题目内容
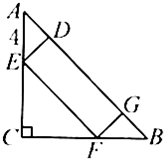 如图,△ABC是等腰直角三角形,已知AE=4cm,长方形DGFE的长DG是它的宽DE的3倍.则△ABC的面积是
如图,△ABC是等腰直角三角形,已知AE=4cm,长方形DGFE的长DG是它的宽DE的3倍.则△ABC的面积是50
50
cm2.分析:因为,△ABC是等腰直角三角形,DGFE是长方形,所以FG=BG,ED=AD,由此把FG看作1份,则EF是3份,DG是3份,AB是5份,那么EF:AB=3:5,由此再根据三角形ABC与三角形ECF相似的性质,得出CE:(CE+4)=3:5,解此比例即可求出CE的值,进而求出△ABC的面积.
解答:解:设CE为x厘米,
x:(x+4)=3:5,
5x=3(x+4),
5x=3x+12,
2x=12,
x=6,
△ABC的面积:(6+4)×(6+4)÷2,
=10×10÷2,
=50(平方厘米),
答:△ABC的面积是50平方厘米;
故答案为:50.
x:(x+4)=3:5,
5x=3(x+4),
5x=3x+12,
2x=12,
x=6,
△ABC的面积:(6+4)×(6+4)÷2,
=10×10÷2,
=50(平方厘米),
答:△ABC的面积是50平方厘米;
故答案为:50.
点评:解答此题的关键是利用长方形的特征与三角形的相似的性质,列出比例,求出所求三角形面积的边,再利用三角形的面积公式解决问题,

练习册系列答案
相关题目
 如图,△ABC是等腰直角三角形,以直角边AB为直径作半圆,与斜边AC交于D,且AB=20厘米,求阴影部分的面积.
如图,△ABC是等腰直角三角形,以直角边AB为直径作半圆,与斜边AC交于D,且AB=20厘米,求阴影部分的面积. 如图,ABC是等腰直角三角形,D是半圆周的中点,BC是半圆的直径.已知AB=BC=10厘米,那么阴影部分的面积是
如图,ABC是等腰直角三角形,D是半圆周的中点,BC是半圆的直径.已知AB=BC=10厘米,那么阴影部分的面积是 如图,ABC是等腰直角三角形,它的内部有两个小正方形,求阴影部分的面积.
如图,ABC是等腰直角三角形,它的内部有两个小正方形,求阴影部分的面积.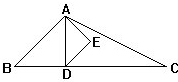 如图三角形ABC是等腰三角形.AB=AC,BAC=120°.三角形ADE是正三角形,点D在BC边上,BD:DC=2:3.当三角形ABC的面积是50cm2时,三角形ADE的面积是多少?
如图三角形ABC是等腰三角形.AB=AC,BAC=120°.三角形ADE是正三角形,点D在BC边上,BD:DC=2:3.当三角形ABC的面积是50cm2时,三角形ADE的面积是多少?