题目内容
【题目】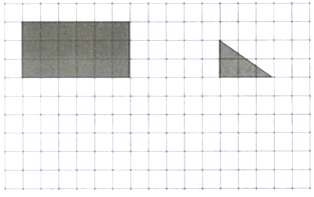
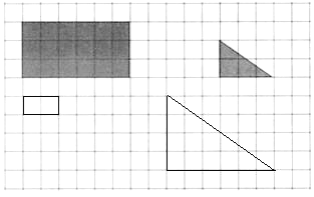
（1）按1：3的比画出长方形缩小后的图形，按2：1的比画出直角三角形放大后的图形。（每个小方格表示1cm2)
（2）沿原来三角形的直角边旋转，可以得到一个圆锥，圆锥的体积最大是多少立方厘米?
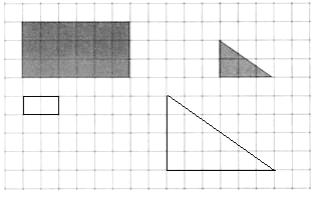
【答案】（1）
（2）18.84立方厘米
【解析】
（1）原来的长方形长是6厘米，宽是3厘米，按1：3的比画出长方形缩小后的图形，缩小后的长方形长是2厘米，宽是1厘米，据此作图；
原来的三角形的两条直角边分别是2厘米，3厘米，按2：1的比画出直角三角形放大后的图形，放大后的两条直角边分别是4厘米，6厘米，据此作图；
（2）要求沿原来三角形的直角边旋转，可以得到一个圆锥，圆锥的体积最大是多少立方厘米，以直角三角形中较长的直角边为圆锥的底面半径，较短直角边为圆锥的高，据此应用公式：V=
πr2h，据此列式解答.
（1）
（2）π×32×2
=×3.14×9×2
=3.14×3×2
=9.42×2
=18.84（立方厘米）
答：圆锥的体积最大是18.84立方厘米.
寒假创新型自主学习第三学期寒假衔接系列答案
【题目】长征造纸厂的生产情况如下表．
时间/天 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
生产量/吨 | 70 | 140 | 210 | 280 | 350 | 420 | 490 |
（1）写出几组这两种量中相对应的两个数的比，求出比值，并比较比值的大小．
（2）说明这个比值所表示的意义．
（3）表中的两种量成正比例关系吗？为什么？
（4）在下面画出它的图像，并根据图像估计一下生产560吨纸大约要用几天时间．
【题目】一列动车在高速铁路上行驶的时间和路程如图．看图填写如表：
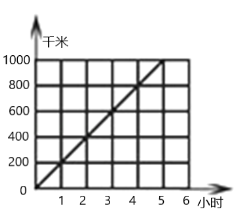
时间/小时 | 3 | （______） |
路程/千米 | （______） | 800 |
①这列动车行驶的时间和路程成________比例
②照这样的速度，行1800千米需要________小时．
【题目】下面是某市水位站发布的8月1日～7日期间，每日下午3时的汛情公告。
根据上面的信息，完成下表。
日期 | 8月1日 | 8月2日 | 8月3日 | 8月4日 | 8月5日 | 8月6日 | 8月7日 |
水位/米 | 41.80 | 42.60 | ____ | ____ | ____ | ____ | ____ |
高于（﹢）或低于（﹣）警戒水位/米 | ﹣0.2 | ﹢0.60 | ____ | ____ | ____ | ____ | ____ |