题目内容
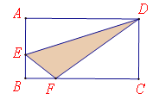
【题目】如图所示,长方形ABCD的长AD为6cm,宽AB为4cm,△ADE、四边形DEBF及△CDF的面积分别相等,则阴影部分面积是多少?
【答案】![]() cm2
cm2
【解析】
阴影部分面积等于四边形DEBF的面积减去△BEF的面积,若要求△BEF的面积需要知道BF、BE的长,可根据△ADE和△CDF的面积分别求出AE、CF,则BE=AB-AE,BF=BC-CF,据此计算求解。
根据题意:
S长方形ABCD=6×4=24(cm2)
S△ADE=S四边形DEBF=S△CDF=![]() S长方形ABCD=24×
S长方形ABCD=24×![]() =8(cm2)
=8(cm2)
∴AE=8×2÷6=![]() (cm),CF=8×2÷4=4(cm)
(cm),CF=8×2÷4=4(cm)
∴BE=AB-AE=4-![]() =
=![]() (cm),BF=BC-CF=6-4=2(cm)
(cm),BF=BC-CF=6-4=2(cm)
∴S阴影=S四边形DEBF-S△BEF
=8-![]() ×2×
×2×![]()
=8-![]()
=![]() (cm2)
(cm2)
答:阴影部分面积是![]() cm2。
cm2。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目