题目内容
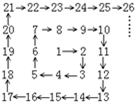 将自然数1,2,3,4…按箭头所指方向顺序排列(如图),依次在2,3,5,7,10…等数的位置处拐弯.
将自然数1,2,3,4…按箭头所指方向顺序排列(如图),依次在2,3,5,7,10…等数的位置处拐弯.(1)如果2算作第一次拐弯处,那么第45次拐弯的数是什么?
(2)从1978到2010的自然数中,恰好在拐弯处的数是什么?
分析:观察拐弯处的数字的规律,既可以得到n个拐弯处的数字的特点,根据题干观察拐弯处的数的规律,可以得到n个拐弯处的数的规律为:
①当n为奇数时为:1+(1+3+5+…+n)=(
)2+1;
②当n为偶数时为:1+2×(1+2+3+…+
)=(1+
)×
+1.
①当n为奇数时为:1+(1+3+5+…+n)=(
| n+1 |
| 2 |
②当n为偶数时为:1+2×(1+2+3+…+
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
解答:解:(1)第45次拐弯处的数是(
)2+1=530.
(2)试算n=89时,拐弯处的数是(
)2+1=2026;n=88时,
拐弯处的数是(1+
)×
+1=1981;
n=87时,拐弯处的数是(
)2+1=1937;
所以1978~2010中,恰在拐弯处的数是1981.
| 45+1 |
| 2 |
(2)试算n=89时,拐弯处的数是(
| 89+1 |
| 2 |
拐弯处的数是(1+
| 88 |
| 2 |
| 88 |
| 2 |
n=87时,拐弯处的数是(
| 87+1 |
| 2 |
所以1978~2010中,恰在拐弯处的数是1981.
点评:观察拐弯处的数字的规律,得到n个拐弯处的数字的特点,是解决本题的关键.

练习册系列答案
相关题目
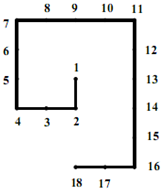 将自然数1、2、3、4^按如图排列:从1开始,下面写2,然后向右转写3、4,然后向上转写5、6、7,依次写下去,这样第一次转弯是2,第2次转弯是4,第3次转弯是7,第4次转弯是11…
将自然数1、2、3、4^按如图排列:从1开始,下面写2,然后向右转写3、4,然后向上转写5、6、7,依次写下去,这样第一次转弯是2,第2次转弯是4,第3次转弯是7,第4次转弯是11…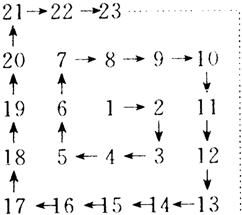 将自然数 1,2,3,…,按如图排列,在“2”处转第一个弯,“3”处转第二个弯,“5”处转第三个弯,….那么在什么处转第二十个弯.
将自然数 1,2,3,…,按如图排列,在“2”处转第一个弯,“3”处转第二个弯,“5”处转第三个弯,….那么在什么处转第二十个弯.