题目内容
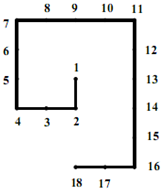 将自然数1、2、3、4^按如图排列:从1开始,下面写2,然后向右转写3、4,然后向上转写5、6、7,依次写下去,这样第一次转弯是2,第2次转弯是4,第3次转弯是7,第4次转弯是11…
将自然数1、2、3、4^按如图排列:从1开始,下面写2,然后向右转写3、4,然后向上转写5、6、7,依次写下去,这样第一次转弯是2,第2次转弯是4,第3次转弯是7,第4次转弯是11…(1)第10次转弯是几?
(2)第2011次转弯是几?
分析:观察题干可知:从数字1开始,每个转弯处的数字是:1、2、4、7、11、16…,这组数据的排列特点是:相邻两数差为1,2,3,4…;由此可得:第一次拐弯处的数字可以写成2=1+1;第二次拐弯处的数字4=1+1+2,第三次拐弯处的数字7=1+1+2+3;第四次拐弯处的数字11=1+1+2+3+4,第五次拐弯处的数字16=1+1+2+3+4+5,…由此可得:第n次拐弯处的数字是1+1+2+3+…+n=1+
,由此即可解答问题.
| n(n+1) |
| 2 |
解答:解:根据题干分析:第n次拐弯处的数字是1+1+2+3+…+n=1+
,
(1)当n=10时,拐弯处的数字是:1+
=1+55=56,
答:第10次拐弯时的数字是56.
(2)当n=2011时,拐弯处的数字是:1+
=1+2023066=2023067,
答:第2011次拐弯时的数字是2023067.
| n(n+1) |
| 2 |
(1)当n=10时,拐弯处的数字是:1+
| 10×(10+1) |
| 2 |
答:第10次拐弯时的数字是56.
(2)当n=2011时,拐弯处的数字是:1+
| 2011×(2011+1) |
| 2 |
答:第2011次拐弯时的数字是2023067.
点评:根据题干推理得出第n次拐弯处的数字的规律,是解决此类问题的关键.

练习册系列答案
相关题目
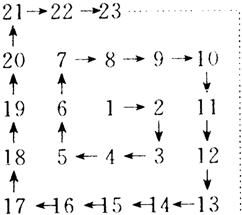 将自然数 1,2,3,…,按如图排列,在“2”处转第一个弯,“3”处转第二个弯,“5”处转第三个弯,….那么在什么处转第二十个弯.
将自然数 1,2,3,…,按如图排列,在“2”处转第一个弯,“3”处转第二个弯,“5”处转第三个弯,….那么在什么处转第二十个弯.