题目内容
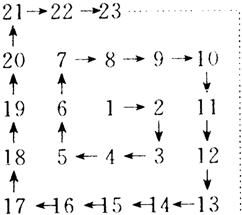 将自然数 1,2,3,…,按如图排列,在“2”处转第一个弯,“3”处转第二个弯,“5”处转第三个弯,….那么在什么处转第二十个弯.
将自然数 1,2,3,…,按如图排列,在“2”处转第一个弯,“3”处转第二个弯,“5”处转第三个弯,….那么在什么处转第二十个弯.分析:观察图形可知:转弯处的数字分别是2,3,5,7,10,13,17,21,…
观察偶数弯数上的数的变化:
第0个弯:1;
第2个弯:3=1+2;
第4个弯:7=1+2+4;
第6个弯:13=1+2+4+6;
…
可以得到规律:第n个弯上的数(n为偶数):1+(2+4+…+n)=1+(2+n)×[(n-2)÷2+1]÷2.
观察偶数弯数上的数的变化:
第0个弯:1;
第2个弯:3=1+2;
第4个弯:7=1+2+4;
第6个弯:13=1+2+4+6;
…
可以得到规律:第n个弯上的数(n为偶数):1+(2+4+…+n)=1+(2+n)×[(n-2)÷2+1]÷2.
解答:解:观察偶数弯数上的数的变化:
第0个弯:1;
第2个弯:3=1+2;
第4个弯:7=1+2+4;
第6个弯:13=1+2+4+6;
…
可以得到规律:第n个弯上的数(n为偶数):1+(2+4+…+n)=1+(2+n)×[(n-2)÷2+1]÷2.
所以第20个弯上的数:1+(2+4…+20)=111.
故在第二十个弯的位置是数111.
第0个弯:1;
第2个弯:3=1+2;
第4个弯:7=1+2+4;
第6个弯:13=1+2+4+6;
…
可以得到规律:第n个弯上的数(n为偶数):1+(2+4+…+n)=1+(2+n)×[(n-2)÷2+1]÷2.
所以第20个弯上的数:1+(2+4…+20)=111.
故在第二十个弯的位置是数111.
点评:本题考查了规律型:数字的变化,解题的关键是找到各个拐弯处的数与相邻拐弯处的数的关系,找出通项公式,从而得解.

练习册系列答案
相关题目
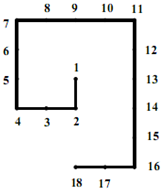 将自然数1、2、3、4^按如图排列:从1开始,下面写2,然后向右转写3、4,然后向上转写5、6、7,依次写下去,这样第一次转弯是2,第2次转弯是4,第3次转弯是7,第4次转弯是11…
将自然数1、2、3、4^按如图排列:从1开始,下面写2,然后向右转写3、4,然后向上转写5、6、7,依次写下去,这样第一次转弯是2,第2次转弯是4,第3次转弯是7,第4次转弯是11…