题目内容
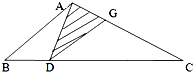如图：在三角形ABC中，CD=3BD，CG=2AG．已知阴影部分的面积是20平方厘米，三角形ABC的面积是多少平方厘米？
解：据分析可知：
S△ADG：S△CDG=1：2，
又因S△ADG=20平方厘米，
所以S△CDG=40平方厘米，
S△ADC=20+40=60平方厘米；
又因S△ADC：S△ABD=3：1，
所以S△ABD=20平方厘米，
因此S△ABC=60+20=80平方厘米；
答：三角形ABC的面积是80平方厘米．
分析：依据等高不等底的三角形的面积等于其对应底的比，则S△ADG：S△CDG=1：2，S△ADC：S△ABD=3：1，从而可以逐步求出三角形ABC的面积．
点评：解答此题的主要依据是：等高不等底的三角形的面积等于其对应底的比．
S△ADG：S△CDG=1：2，
又因S△ADG=20平方厘米，
所以S△CDG=40平方厘米，
S△ADC=20+40=60平方厘米；
又因S△ADC：S△ABD=3：1，
所以S△ABD=20平方厘米，
因此S△ABC=60+20=80平方厘米；
答：三角形ABC的面积是80平方厘米．
分析：依据等高不等底的三角形的面积等于其对应底的比，则S△ADG：S△CDG=1：2，S△ADC：S△ABD=3：1，从而可以逐步求出三角形ABC的面积．
点评：解答此题的主要依据是：等高不等底的三角形的面积等于其对应底的比．
练习册系列答案
相关题目
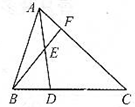如图，在三角形ABC中，BD：DC=1：2，AE=ED，则AF：FC=（ ）
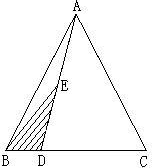如图：在三角形ABC中，BD=
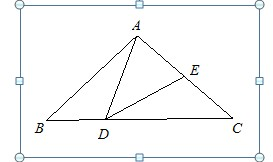如图，在三角形ABC中，CD的长是BD长的2倍，E是AC的中点，则三角形ABC的面积是三角形ADE面积的（ ） 倍．
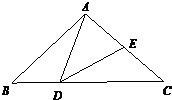如图，在三角形ABC中，CD的长是BD长的2倍，E是AC的中点，则三角形ABC的面积是三角形ADE面积的
如图，在三角形ABC中，D、E为两个三等分点，F为AB的中点，若△EDF的面积是12平方厘米，则△ABC的面积是（ ）平方厘米．