题目内容
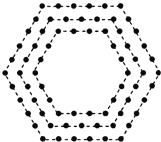
【题目】在学校的运动会上,同学们集体表演一个节目,站成了一个空心的正六边形阵列,与图中的阵列类似.从外向内一共8层,依次站着两层六年级的同学,两层五年级的同学,两层四年级的同学以及两层三年级的同学.已知参加表演的六年级同学有126名,请问:
(1)最外层有多少人?
(2)现在阵列中一共有多少人?
(3)如果想要一、二年级的同学把这个空心阵列填满,还需要多少人?
【答案】(1)66人.(2)360人.(3)37人.
【解析】
试题分析:(1)相邻两边的人数相差1,所以相邻的两圈的人数相差6,因为六年级同学有126名,站了两层,所以根据和差问题的解答方法即可求出最外层有多少人:(126+6)÷2=66(人);
(2)最外层有66人,最内层有66﹣6×(8﹣1)=24(人),然后根据高斯求和公式解答即可;
(3)如果想要一、二年级的同学把这个空心阵列填满,里面空缺的最外一层有24﹣6=18(人),最里面有6人,有(18﹣6)÷6+1=3层,然后根据高斯求和公式解答,最后加上最中心的一人即可.
解:(1)(126+6)÷2
=132÷2
=66(人);
答:最外层有66人.
(2)最内层有66﹣6×(8﹣1)
=66﹣42
=24(人)
(24+66)×8÷2
=90×4
=360(人);
答:现在阵列中一共有360人.
(3)里面空缺的最外一层有24﹣6=18(人),最里面有6人,有(18﹣6)÷6+1=3(层),
(18+6)×3÷2+1
=36+1
=37(人)
答:如果想要一、二年级的同学把这个空心阵列填满,还需要37人.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目