 某系统采用低息贷款的方式对所属企业给予扶持,该系统制定了评分标准,并根据标准对企业进行评估,然后依据评估得分将这些企业分别定为优秀、良好、合格、不合格四个等级,并根据等级分配相应的低息贷款数额.为了更好地掌握贷款总额,该系统随机抽查了所属的部分企业,以下图表给出了有关数据(将频率看作概率)
某系统采用低息贷款的方式对所属企业给予扶持,该系统制定了评分标准,并根据标准对企业进行评估,然后依据评估得分将这些企业分别定为优秀、良好、合格、不合格四个等级,并根据等级分配相应的低息贷款数额.为了更好地掌握贷款总额,该系统随机抽查了所属的部分企业,以下图表给出了有关数据(将频率看作概率)
| 评估得分 | [50,60) | [60,70) | [70,80) | [80,90) |
| 评定类型 | 不合格 | 合格 | 良好 | 优秀 |
| 贷款金额(万元) | 0 | 200 | 400 | 800 |
(2)对照标准,企业进行了整改,整改后,如果优秀企业数量不变,不合格企业、合格企业、良好企业的数量成等差数列.要使所属企业获得贷款的平均值(即数学期望)不低于410万元,那么整改后不合格企业占企业总数百分比的最大值是多少?
 为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
| 性别 是否 达标 | 男 | 女 | 合计 |
| 达标 | a=24 | b=________ | ________ |
| 不达标 | c=________ | d=12 | ________ |
| 合计 | ________ | ________ | n=50 |
(Ⅱ) 根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如附表:
根据上表数据,能否有99%的把握认为“体育达标与性别有关”?若有,你能否提出一个更好的解决方法来?
附:K2=
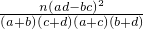 .
.| P(K2≥K) | 0.050 | 0.010 | 0.001 |
| K | 3.841 | 6.625 | 10.828 |
 (4n-1)
(4n-1) (2n-1)
(2n-1) (4n-1)
(4n-1)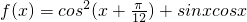 ,.
,. ,
, ],使得不等式f(x0)<m成立,求m的取值范围.
],使得不等式f(x0)<m成立,求m的取值范围.
 B
B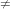 B
B ,
, 满足|
满足| ,且(
,且(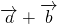 )⊥(
)⊥(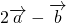 )=0,则
)=0,则