题目内容
已知函数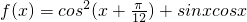 ,.
,.
(1)求f(x)的最小正周期和图象的对称中心;
(2)若存在x0∈[ ,
, ],使得不等式f(x0)<m成立,求m的取值范围.
],使得不等式f(x0)<m成立,求m的取值范围.
解: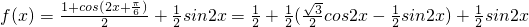 =
=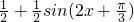
(1)f(x)的最小正周期为π,令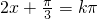 ,得
,得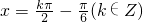 ,
,
所以函数f(x)的图象的对称中心为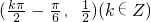 .(6分)
.(6分)
(2)由x0∈[ ,
, ],得
],得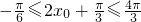 ,则
,则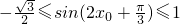 ,
,
于是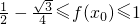 ,而若存在x0∈[
,而若存在x0∈[ ,
, ]使得不等式f(x0)<m成立,
]使得不等式f(x0)<m成立,
只需m>f(x0)min,即m的取值范围为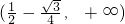 .(6分)
.(6分)
分析:利用二倍角公式化简2的表达式为一个角的一个三角函数的形式,
(1)直接利用周期公式求出函数的周期,结合三角函数的对称中心求解即可.
(2)x0∈[ ,
, ],求出
],求出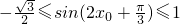 ,即可求出m的取值范围.
,即可求出m的取值范围.
点评:本题是中档题,考查三角函数的化简求值,注意区别恒成立问题与本题的区别.考查计算能力.
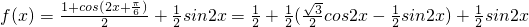 =
=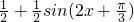
(1)f(x)的最小正周期为π,令
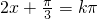 ,得
,得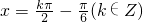 ,
,所以函数f(x)的图象的对称中心为
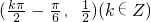 .(6分)
.(6分)(2)由x0∈[
 ,
, ],得
],得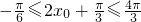 ,则
,则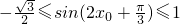 ,
,于是
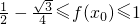 ,而若存在x0∈[
,而若存在x0∈[ ,
, ]使得不等式f(x0)<m成立,
]使得不等式f(x0)<m成立,只需m>f(x0)min,即m的取值范围为
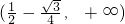 .(6分)
.(6分)分析:利用二倍角公式化简2的表达式为一个角的一个三角函数的形式,
(1)直接利用周期公式求出函数的周期,结合三角函数的对称中心求解即可.
(2)x0∈[
 ,
, ],求出
],求出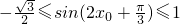 ,即可求出m的取值范围.
,即可求出m的取值范围.点评:本题是中档题,考查三角函数的化简求值,注意区别恒成立问题与本题的区别.考查计算能力.

练习册系列答案
相关题目