(2)使用液化气的出租车,当前的液化气价格为4.95元/千克. 假设每千克液化气能行驶15千米,行驶t天所耗的液化气费用为p元,请写出p关于t的函数关系式;
(3)若出租车要改装为使用液化气,每辆需配置成本为8000元的设备.根据近阶段汽油和液化气的价位,在(1)、(2)的基础上,问需要几天才能收回改装成本?
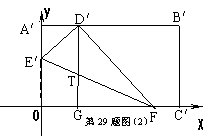
得 分 评卷人 如图,已知抛物线y=ax2+4ax+t(a>0)交x轴于 A、B两点,交y轴于点C,点B的坐标为(-1,0). (1)求此抛物线的对称轴及点A的坐标; (2)过点C作x轴的平行线交抛物线的对称轴于点P, 你能判断四边形ABCP是什么四边形吗?请证明你的结论; 得 分 评卷人 善于学习的小敏查资料知道:对应角相等,对应边成比例的两 个梯形,叫做相似梯形.他想到“平行于三角形一边的直线和其 他两边相交,所构成的三角形与原三角形相似”,提出如下两个 问题,你能帮助解决吗? 问题一 平行于梯形底边的直线截两腰所得的小梯形和原梯形是否相似? (1)从特殊情形入手探究.假设梯形ABCD中, AD∥BC,AB=6,BC=8,CD=4, AD=2,MN是中位线(如图①).根据相似梯形的定义,请你说明梯形AMND与梯形ABCD是否相似? (2)一般结论:平行于梯形底边的直线截两腰所得的梯形与原梯形______________
(填“相似”或“不相似”或“相似性无法确定”.不要求证明) . 问题二 平行于梯形底边的直线截两腰所得的两个小梯形是否相似? (1)从特殊平行线入手探究.梯形的中位线截两腰所得的两个小梯形______________
(填“相似”或“不相似”或“相似性无法确定”.不要求证明). (2)从特殊梯形入手探究.同上假设,梯形ABCD中,AD∥BC,AB=6,BC=8,CD=4,AD=2,你能找到与梯形底边平行的直线PQ(点P,Q在梯形的两腰上,如图②), 使得梯形APQD与梯形PBCQ相似吗? 请根据相似梯形的定义说明理由. 平行于梯形底边的直线PQ,使截得的两个小梯形相似. 若存在,则确定这条平行线位置的条件是= (不妨设AD= a,BC= b,AB=c,CD= d.不要求证明 ) .
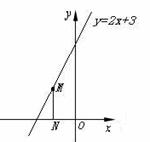 14.如图,已知AB∥CD,直线EF分别交 AB、CD于点
E,F,EG平分∠BEF交CD于点G,如果∠1=50°,那么∠2的度数是 ▲ 度.
14.如图,已知AB∥CD,直线EF分别交 AB、CD于点
E,F,EG平分∠BEF交CD于点G,如果∠1=50°,那么∠2的度数是 ▲ 度. 这次成绩的众数是 ▲ .
这次成绩的众数是 ▲ .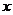 2+4
2+4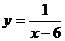 的表达式中,自变量
的表达式中,自变量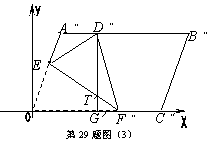
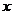 ,
,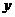 )的坐标
)的坐标