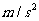7、反三角函数的主值区间:
|
反三角函数 |
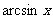 |
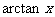 |
 |
|
定义域 |
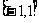 |
R |
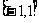 |
|
主值区间(值域) |
 |
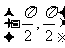 |
 |
|
还原性 |
sin(arcsinx)=x,(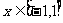 ) )arcsinx=x,( 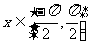 ) ) |
tan(arctanx)=x,
(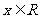 ) )arctanx=x,( 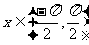 ) ) |
cos(arccosx)=x,(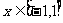 ) )arccosx=x,( 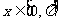 ) ) |
|
公式 |
arcsin(-x)=-arcsinx |
arctan(-x)=-arctanx |
arcos(-x)=  -arccosx -arccosx |
8,圆的三种方程:
|
名称 |
形式 |
圆心 |
半径 |
条件 |
|
标准方程 |
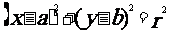 |
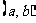 |
r |
r>0 |
|
参数方程 |
 |
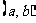 |
r |
r>0 |
|
一般方程 |
 |
 |
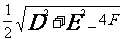 |
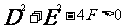 |
(1)点 与圆
与圆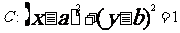 的位置关系:
的位置关系:
若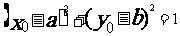 ,则点
,则点 在圆C上;
在圆C上;
若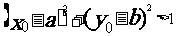 ,则点
,则点 在圆C外;
在圆C外;
若 ,则点
,则点 在圆C内;
在圆C内;
(2)直线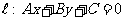 与圆
与圆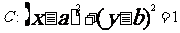 的位置关系:
的位置关系:
①联立 
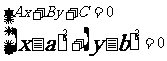 消去y得:
消去y得:
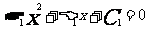 ,则
,则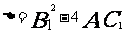 ,直线
,直线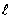 与圆
与圆 的位置关系:
的位置关系:
 相交;
相交;  相切 ;
相切 ;
 相离 。
相离 。
② 圆心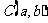 到直线
到直线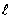 的距离为
的距离为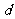 ,则直线
,则直线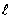 与圆
与圆 的位置关系:
的位置关系:
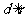 相交;
相交;
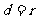 相切 ;
相切 ;
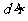 相离 。
相离 。
(3)圆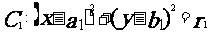 与圆
与圆 的位置关系:
的位置关系:
 相交;
相交;
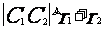 相离;
相离;
 外切;
外切;
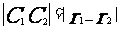 内切。
内切。
(4)半弦长与弦心距的平方和等于半径的平方。
(5)弦的垂直平分线经过圆心。
(6)圆心到切线的距离等于半径。
9,椭圆
|
第一定义 |
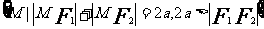 |
|
|||
|
第二定义 |
 |
|
|||
|
标准方程 |
 |
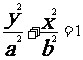 |
|
||
|
参数方程 |
|
|
|
||
|
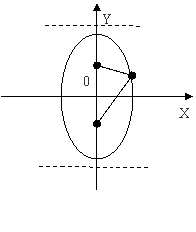
图 象 |
|
  |
|
||
 关 系 关 系 |
 |
|
|||
|
范 围 |
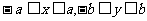 |
 |
|
||
|
顶 点 |
 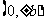 |
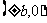 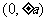 |
|
||
|
对 称
性 |
  关于 关于 轴成轴对称、关于原点成中心对称 轴成轴对称、关于原点成中心对称 |
|
|||
|
离 心
率 |
 |
|
|||
|
焦 点 |
 |
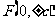 |
 |
||
|
准 线 |
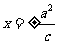 |
 |
|
||
|
焦点三角形面积公式 |
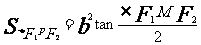 |
|
|||
(1)点 与椭圆C:
与椭圆C: 的位置关系:
的位置关系:
若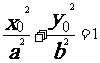 ,则点
,则点 在椭圆C上;
在椭圆C上;
若 ,则点
,则点 在椭圆C外;
在椭圆C外;
若 ,则点
,则点 在椭圆C内;
在椭圆C内;
(2)直线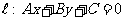 与椭圆C:
与椭圆C: 的位置关系判断:用
的位置关系判断:用 法。
法。
10,双曲线
|
第一定义 |
 |
||||||||||||||||||
|
第二定义 |
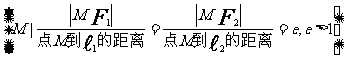 |
||||||||||||||||||
|
方 程 |
 ( (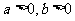 ) ) |
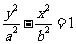 ( (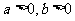 ) ) |
|||||||||||||||||
|
图 象 |
|
     
|
|||||||||||||||||
 关 系 关 系 |
 |
||||||||||||||||||
|
范 围 |
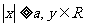 |
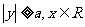 |
|||||||||||||||||
|
顶 点 |
 |
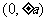 |
|||||||||||||||||
|
对 称 性 |
关于 轴成轴对称、关于原点成中心对称 轴成轴对称、关于原点成中心对称 |
||||||||||||||||||
|
渐 近 线 |
 |
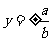 |
|||||||||||||||||
|
离 心 率 |
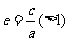 |
||||||||||||||||||
|
焦 点 |
 |
 |
|||||||||||||||||
|
准 线 |
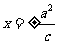 |
 |
|||||||||||||||||
|
焦点三角形面积公式 |
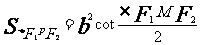 |
11,抛物线
|
定义 |
平面内,到定点F的距离与到定直线 的距离相等的点的轨迹。 的距离相等的点的轨迹。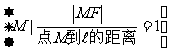 |
|||
|
方程 |
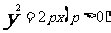 |
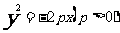 |
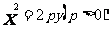 |
 |
|
图
形 |
 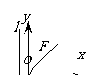 |
 |
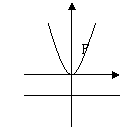  |
 |
|
焦点坐标 |
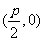 |
 |
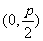 |
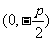 |
|
准线方程 |
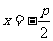 |
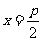 |
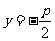 |
 |
|
范围 |
 |
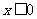 |
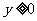 |
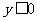 |
|
对称性 |
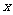 轴 轴 |
 轴 轴 |
||
|
顶点 |
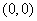 |
|||
|
离心率 |
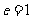 |

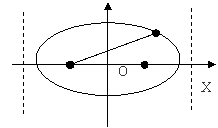





 度是指长度的计量标准,单位有丈、尺、寸等;
度是指长度的计量标准,单位有丈、尺、寸等;

 商鞅铜方升
商鞅铜方升


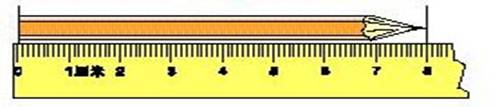
 1790年:巴黎会议约定:通过巴黎的地球子午线全长的四千万分之一定义为1米。
1790年:巴黎会议约定:通过巴黎的地球子午线全长的四千万分之一定义为1米。







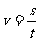 ,那公式中的位移单位是m,时间单位是秒,速度单位是米每秒。如果我们计算时时间单位用小时,位移用米,速度用米每秒,那公式就得变形为
,那公式中的位移单位是m,时间单位是秒,速度单位是米每秒。如果我们计算时时间单位用小时,位移用米,速度用米每秒,那公式就得变形为
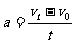 ,速度用米每秒做单位,时间用秒做单位,得出加速度的单位就是米每二次方秒。
,速度用米每秒做单位,时间用秒做单位,得出加速度的单位就是米每二次方秒。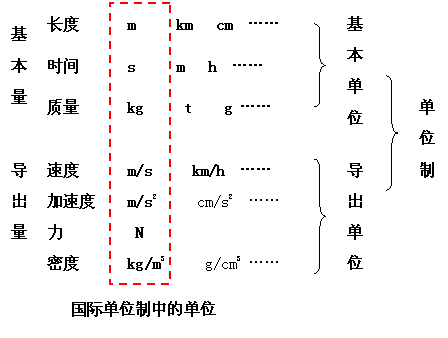
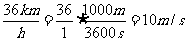
 ____________
____________