摘要:若存在,试给出证明;若不存在,请说明理由四.3答案:
网址:http://m.1010jiajiao.com/timu_id_94159[举报]
对于函数y=f(x),定义:若存在非零常数M、T,使函数f(x)对定义域内的任意实数x,都满足f(x+T)-f(x)=M,则称函数y=f(x)是准周期函数,常数T称为函数y=f(x)的一个准周期.如:函数f(x)=2x+sinx是以T=2π为一个准周期且M=4π的准周期函数.

(1)试判断2π是否是函数f(x)=sinx的准周期,说明理由;
(2)证明函数f(x)=x+(-1)x(x∈Z)是准周期函数,并求出它的一个准周期和相应的M的值;
(3)请你给出一个准周期函数(不同于题设和(2)中函数),指出它的一个准周期和一些性质,并画出它的大致图像
对于函数y=f(x),定义:若存在非零常数M、T,使函数f(x)对定义域内的任意实数x,都满足f(x+T)-f(x)=M,则称函数y=f(x)是准周期函数,常数T称为函数y=f(x)的一个准周期.如函数f(x)=x+(-1)x(x∈Z)是以T=2为一个准周期且M=2的准周期函数.
(1)试判断2π是否是函数f(x)=sinx的准周期,说明理由;
(2)证明函数f(x)=2x+sinx是准周期函数,并求出它的一个准周期和相应的M的值;
(3)请你给出一个准周期函数(不同于题设和(2)中函数),指出它的一个准周期和一些性质,并画出它的大致图象.
查看习题详情和答案>>
(1)试判断2π是否是函数f(x)=sinx的准周期,说明理由;
(2)证明函数f(x)=2x+sinx是准周期函数,并求出它的一个准周期和相应的M的值;
(3)请你给出一个准周期函数(不同于题设和(2)中函数),指出它的一个准周期和一些性质,并画出它的大致图象.
由下面四个图形中的点数分别给出了四个数列的前四项,将每个图形的层数增加可得到这四个数列的后继项.按图中多边形的边数依次称这些数列为“三角形数列”、“四边形数列” ,将构图边数增加到
,将构图边数增加到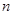 可得到“
可得到“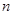 边形数列”,记它的第
边形数列”,记它的第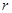 项为
项为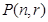 ,
,
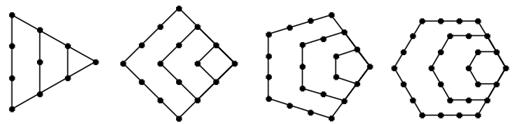
1,3,6,10 1,4,9,16 1,5,12,22 1,6,15,28
(1)
求使得 的最小
的最小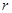 的取值;
的取值;
(2)
试推导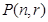 关于
关于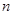 、
、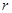 的解析式;
的解析式;
( 3) 是否存在这样的“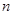 边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
查看习题详情和答案>>
 ,将构图边数增加到
,将构图边数增加到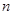 可得到“
可得到“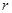 项为
项为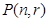 ,
,
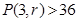 的最小
的最小 在实数集R上,函数
在实数集R上,函数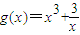 在
在 上是不是有界函数?若是,请给出证明;若不是,请说出理由.
上是不是有界函数?若是,请给出证明;若不是,请说出理由.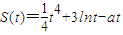 ,要使在
,要使在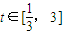 上每一时刻的瞬时速度的绝对值都不大于13,求实数a的取值范围.
上每一时刻的瞬时速度的绝对值都不大于13,求实数a的取值范围.