题目内容
定义在D上的函数,如果满足:存在常数M>0,对任意x∈D都有|f(x)|≤M成立,则称f(x)是D上的有界函数.(1)试判断函数
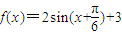 在实数集R上,函数
在实数集R上,函数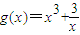 在
在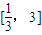 上是不是有界函数?若是,请给出证明;若不是,请说出理由.
上是不是有界函数?若是,请给出证明;若不是,请说出理由.(2)若已知某质点的运动距离S与时间t的关系为
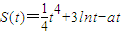 ,要使在
,要使在 上每一时刻的瞬时速度的绝对值都不大于13,求实数a的取值范围.
上每一时刻的瞬时速度的绝对值都不大于13,求实数a的取值范围.
【答案】分析:(1)先根据函数f(x)的最大值和最小值可判断M的值,进而得到f(x)在R上是有界函数;对于函数g(x)进行求导,令导函数等于0求x的值,然后根据导函数的正负判断函数的单调性进而得到g(x)在[ ,1]上最大和最小值,然后令M=两最值绝对值较大的一个,进而可判断是有界函数.
,1]上最大和最小值,然后令M=两最值绝对值较大的一个,进而可判断是有界函数.
(2)对函数S(t)进行求导得到瞬时速度,然后令瞬时速度的绝对值都小于等于13在 上恒成立,然后转化为a关于t的关系式a(t),使得a大于等于a(t)的最大值或小于等于a(t)的最小值,进而得到a的范围.
上恒成立,然后转化为a关于t的关系式a(t),使得a大于等于a(t)的最大值或小于等于a(t)的最小值,进而得到a的范围.
解答:解:(1)∵ 在R上的最大值为5,最小值为-1,
在R上的最大值为5,最小值为-1,
存在常数M=5,对任意x∈R都有|f(x)|≤M,∴f(x)在R上是有界函数.
∵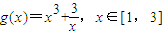 ,∴
,∴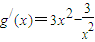 ,
,
由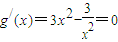 ,得x=1或x=-1
,得x=1或x=-1
所以g(x)在[ ,1]上单调递减,g(x)在[1,3]上单调递增,
,1]上单调递减,g(x)在[1,3]上单调递增,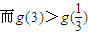
∴g(x)在[ ,3]上的最大值为g(3)=28,最小值为g(1)=4
,3]上的最大值为g(3)=28,最小值为g(1)=4
所以存在常数M=28,对任意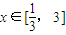 都有|g(x)|≤M,∴g(x)是
都有|g(x)|≤M,∴g(x)是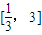 上是有界函数.
上是有界函数.
(2)因为运动方程为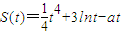 ,所以瞬时速度
,所以瞬时速度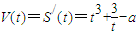
由当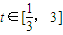 时,|V(t)|≤13恒成立,即
时,|V(t)|≤13恒成立,即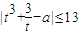 对
对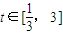 恒成立
恒成立
即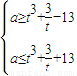 对
对 恒成立,由(1)可得15≤a≤17
恒成立,由(1)可得15≤a≤17
所以实数a的取值范围[15,17]
点评:本题主要考查函数的有界性和函数的单调性与其导函数的正负之间的关系.导数是由高等数学下放到高中的新内容,每年必考,要给予重视.
 ,1]上最大和最小值,然后令M=两最值绝对值较大的一个,进而可判断是有界函数.
,1]上最大和最小值,然后令M=两最值绝对值较大的一个,进而可判断是有界函数.(2)对函数S(t)进行求导得到瞬时速度,然后令瞬时速度的绝对值都小于等于13在
 上恒成立,然后转化为a关于t的关系式a(t),使得a大于等于a(t)的最大值或小于等于a(t)的最小值,进而得到a的范围.
上恒成立,然后转化为a关于t的关系式a(t),使得a大于等于a(t)的最大值或小于等于a(t)的最小值,进而得到a的范围.解答:解:(1)∵
 在R上的最大值为5,最小值为-1,
在R上的最大值为5,最小值为-1,存在常数M=5,对任意x∈R都有|f(x)|≤M,∴f(x)在R上是有界函数.
∵
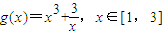 ,∴
,∴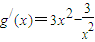 ,
,由
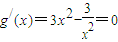 ,得x=1或x=-1
,得x=1或x=-1所以g(x)在[
 ,1]上单调递减,g(x)在[1,3]上单调递增,
,1]上单调递减,g(x)在[1,3]上单调递增,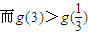
∴g(x)在[
 ,3]上的最大值为g(3)=28,最小值为g(1)=4
,3]上的最大值为g(3)=28,最小值为g(1)=4所以存在常数M=28,对任意
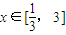 都有|g(x)|≤M,∴g(x)是
都有|g(x)|≤M,∴g(x)是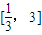 上是有界函数.
上是有界函数.(2)因为运动方程为
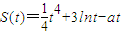 ,所以瞬时速度
,所以瞬时速度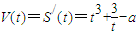
由当
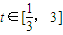 时,|V(t)|≤13恒成立,即
时,|V(t)|≤13恒成立,即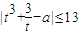 对
对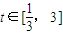 恒成立
恒成立即
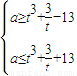 对
对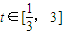 恒成立,由(1)可得15≤a≤17
恒成立,由(1)可得15≤a≤17所以实数a的取值范围[15,17]
点评:本题主要考查函数的有界性和函数的单调性与其导函数的正负之间的关系.导数是由高等数学下放到高中的新内容,每年必考,要给予重视.

练习册系列答案
相关题目

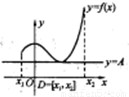
 如右图所示,定义在D上的函数f(x),如果满足:对?x∈D,常数A,都有f(x)≥A成立,则称函数f(x)在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)
如右图所示,定义在D上的函数f(x),如果满足:对?x∈D,常数A,都有f(x)≥A成立,则称函数f(x)在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)
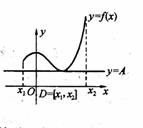 (本题满分12)如右图所示,定义在D上的函数
(本题满分12)如右图所示,定义在D上的函数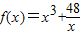 在(0,+∞)上是否有下界?并说明理由;
在(0,+∞)上是否有下界?并说明理由;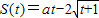 ,要使在t∈[0,+∞)上的每一时刻该质点的瞬时速度是以
,要使在t∈[0,+∞)上的每一时刻该质点的瞬时速度是以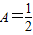 为下界的函数,求实数a的取值范围.
为下界的函数,求实数a的取值范围.