摘要:(Ⅲ)当时.证明存在.使得不等式对任意的恒成立.
网址:http://m.1010jiajiao.com/timu_id_85501[举报]
设函数 。
。
(1)当 时,已知
时,已知 在
在 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(2)当 是整数时,存在实数
是整数时,存在实数 ,使得
,使得 是
是 的最大值,且
的最大值,且 是
是 的最小值,求所有这样的实数对
的最小值,求所有这样的实数对 ;
;
(3)定义函数 ,则当
,则当 取得最大值时的自变量
取得最大值时的自变量 的值依次构成一个等差数列,写出该等差数列的通项公式(不必证明)。
的值依次构成一个等差数列,写出该等差数列的通项公式(不必证明)。
查看习题详情和答案>>
网址:http://m.1010jiajiao.com/timu_id_85501[举报]
设函数 。
。
(1)当 时,已知
时,已知 在
在 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(2)当 是整数时,存在实数
是整数时,存在实数 ,使得
,使得 是
是 的最大值,且
的最大值,且 是
是 的最小值,求所有这样的实数对
的最小值,求所有这样的实数对 ;
;
(3)定义函数 ,则当
,则当 取得最大值时的自变量
取得最大值时的自变量 的值依次构成一个等差数列,写出该等差数列的通项公式(不必证明)。
的值依次构成一个等差数列,写出该等差数列的通项公式(不必证明)。
查看习题详情和答案>>
 .
.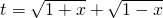 ,求t的取值范围;
,求t的取值范围;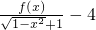
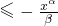 成立的最小正数α=2,并求此时的最小正数β.
成立的最小正数α=2,并求此时的最小正数β.