题目内容
设函数 。
。
(1)当 时,已知
时,已知 在
在 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(2)当 是整数时,存在实数
是整数时,存在实数 ,使得
,使得 是
是 的最大值,且
的最大值,且 是
是 的最小值,求所有这样的实数对
的最小值,求所有这样的实数对 ;
;
(3)定义函数 ,则当
,则当 取得最大值时的自变量
取得最大值时的自变量 的值依次构成一个等差数列,写出该等差数列的通项公式(不必证明)。
的值依次构成一个等差数列,写出该等差数列的通项公式(不必证明)。
【答案】
解:(1)当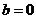 时,
时,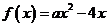 ,
1分
,
1分
若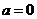 ,则
,则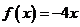 在
在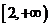 上递减,不合题意,舍去;
1分
上递减,不合题意,舍去;
1分
故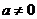 ,要使
,要使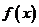 在
在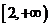 上单调递增,则
上单调递增,则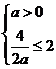 ,即
,即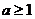 ; 4分
; 4分
(2)若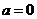 ,则
,则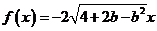 无最大值,不合题意,故
无最大值,不合题意,故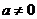 , 1分
, 1分
于是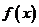 为二次函数,
为二次函数,
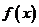 有最大值
有最大值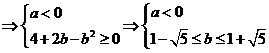 ,
,
此时,当 时,
时,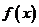 取到最大值,
3分
取到最大值,
3分
显然,当且仅当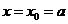 时,
时,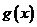 取到最小值,故
取到最小值,故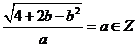 , 1分
, 1分
于是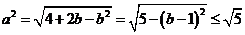
又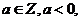 所以
所以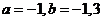 ,
,
所以满足题意的实数对为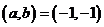 ,或
,或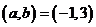 ; 3分
; 3分
(3)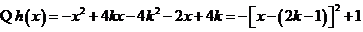 2分
2分
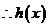 取得最大值时
取得最大值时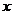 的值为
的值为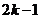 (
(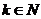 ),
),
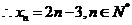 。
2分
。
2分

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 .
. 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程; 时,求函数
时,求函数 ,若对于
,若对于 [1,2],
[1,2], [0,1],使
[0,1],使 成立,求实数
成立,求实数 的取值范围.
的取值范围. .
. 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程; 时,求函数
时,求函数 ,若对于
,若对于 [1,2],
[1,2], [0,1],使
[0,1],使 成立,求实数
成立,求实数 的取值范围.
的取值范围. 。
。 时,求
时,求 的单调区间。
的单调区间。 上的最大值为
上的最大值为 ,求
,求 的值。
的值。 。
。 时,求函数
时,求函数 的最小值;
的最小值; 时,试判断函数
时,试判断函数