题目内容
已知函数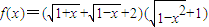 .
.(Ⅰ)设
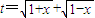 ,求t的取值范围;
,求t的取值范围;(Ⅱ)关于x的方程f(x)-m=0,x∈[0,1],存在这样的m值,使得对每一个确定的m,方程都有唯一解,求所有满足条件的m.
(Ⅲ)证明:当0≤x≤1时,存在正数β,使得不等式
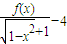
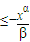 成立的最小正数α=2,并求此时的最小正数β.
成立的最小正数α=2,并求此时的最小正数β.
【答案】分析:(Ⅰ)两边平方,借助于函数定义域x∈[-1,1],求得t 的取值范围是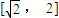 ;(Ⅱ)只需要求出函数x∈[0,1]的值域即可知m值的范围;(Ⅲ)将问题等价转化为
;(Ⅱ)只需要求出函数x∈[0,1]的值域即可知m值的范围;(Ⅲ)将问题等价转化为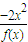
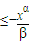 恒成立,∴
恒成立,∴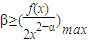 =
=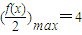 ,从而求出最小正数.
,从而求出最小正数.
解答:解:(Ⅰ)函数定义域x∈[-1,1], ,∵t≥0,∴
,∵t≥0,∴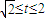 ,即t 的取值范围是
,即t 的取值范围是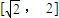 (Ⅱ)
(Ⅱ)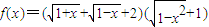 ,由(Ⅰ)
,由(Ⅰ)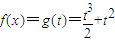 ,
,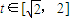 ,g(t) 在
,g(t) 在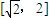 单调递增,所以
单调递增,所以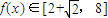 .设x1,x2∈[0,1],x1≠x2,则1-x12≠1-x22,即
.设x1,x2∈[0,1],x1≠x2,则1-x12≠1-x22,即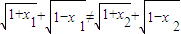 ,即t1≠t2.故存在m,使得对每一个
,即t1≠t2.故存在m,使得对每一个 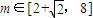 ,方程都有唯一解x∈[0,1].
,方程都有唯一解x∈[0,1].
(Ⅲ)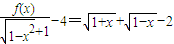 =
=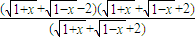 =
=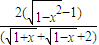 =
=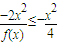 .以下证明,对0<α0,不等式
.以下证明,对0<α0,不等式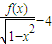
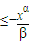 (0≤x≤1)不成立.反之,由
(0≤x≤1)不成立.反之,由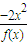
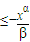 ,亦即x2-α
,亦即x2-α 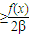 成立,因为2-α>0,
成立,因为2-α>0,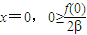 ,但f(0)=8,这是不可能的.这说明α=2 是满足条件的最小正数.这样,不等式
,但f(0)=8,这是不可能的.这说明α=2 是满足条件的最小正数.这样,不等式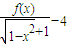
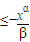 (x∈[0,1]) 恒成立,即
(x∈[0,1]) 恒成立,即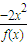
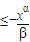 恒成立,∴
恒成立,∴ =
=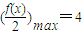 ,最小正数β=4
,最小正数β=4
点评:本题主要考查了函数的最值及其几何意义,以及分类讨论的思想,解题的关键是对于恒成立的理解,是一道综合题
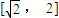 ;(Ⅱ)只需要求出函数x∈[0,1]的值域即可知m值的范围;(Ⅲ)将问题等价转化为
;(Ⅱ)只需要求出函数x∈[0,1]的值域即可知m值的范围;(Ⅲ)将问题等价转化为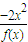
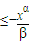 恒成立,∴
恒成立,∴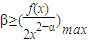 =
=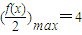 ,从而求出最小正数.
,从而求出最小正数.解答:解:(Ⅰ)函数定义域x∈[-1,1],
 ,∵t≥0,∴
,∵t≥0,∴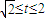 ,即t 的取值范围是
,即t 的取值范围是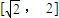 (Ⅱ)
(Ⅱ)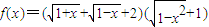 ,由(Ⅰ)
,由(Ⅰ)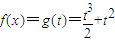 ,
,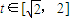 ,g(t) 在
,g(t) 在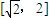 单调递增,所以
单调递增,所以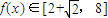 .设x1,x2∈[0,1],x1≠x2,则1-x12≠1-x22,即
.设x1,x2∈[0,1],x1≠x2,则1-x12≠1-x22,即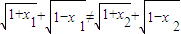 ,即t1≠t2.故存在m,使得对每一个
,即t1≠t2.故存在m,使得对每一个 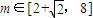 ,方程都有唯一解x∈[0,1].
,方程都有唯一解x∈[0,1].(Ⅲ)
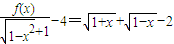 =
=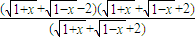 =
=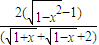 =
=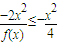 .以下证明,对0<α0,不等式
.以下证明,对0<α0,不等式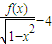
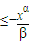 (0≤x≤1)不成立.反之,由
(0≤x≤1)不成立.反之,由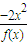
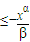 ,亦即x2-α
,亦即x2-α 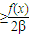 成立,因为2-α>0,
成立,因为2-α>0,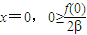 ,但f(0)=8,这是不可能的.这说明α=2 是满足条件的最小正数.这样,不等式
,但f(0)=8,这是不可能的.这说明α=2 是满足条件的最小正数.这样,不等式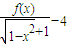
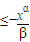 (x∈[0,1]) 恒成立,即
(x∈[0,1]) 恒成立,即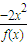
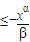 恒成立,∴
恒成立,∴ =
=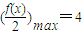 ,最小正数β=4
,最小正数β=4点评:本题主要考查了函数的最值及其几何意义,以及分类讨论的思想,解题的关键是对于恒成立的理解,是一道综合题

练习册系列答案
相关题目
 .
. 的值域.
的值域.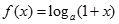 ,
,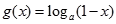 ,
,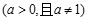 .
.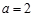 ,函数
,函数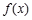 的定义域为
的定义域为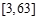 ,求函数
,求函数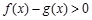 的
的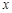 的取值范围.
的取值范围. 定义域为
定义域为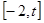 (
(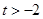 ),设
),设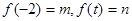 .
.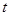 的取值范围,使得函数
的取值范围,使得函数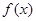 在
在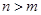 ;
;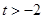 ,总存在
,总存在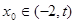 ,满足
,满足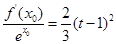 ,并确定这样的
,并确定这样的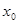 的个数.
的个数.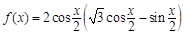 .
.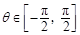 ,且
,且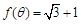 ,求
,求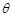 的值;
的值;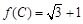 ,且△ABC的面积为
,且△ABC的面积为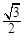 ,求sinA+sinB的值.
,求sinA+sinB的值. .
. 在
在 上单调递增,求
上单调递增,求 的取值范围。
的取值范围。 与
与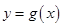 的图象有两个不同的交点M、N,求
的图象有两个不同的交点M、N,求 轴的垂线分别与
轴的垂线分别与 的图像和
的图像和 的图像交S、T点,以S为切点作
的图像交S、T点,以S为切点作 ,以T为切点作
,以T为切点作 .是否存在实数
.是否存在实数