网址:http://m.1010jiajiao.com/timu_id_85386[举报]
(I)求椭圆的方程;
(Ⅱ)若直线l同时满足下列三个条件:①与直线B1F平行;②与椭圆交于两个不同的点P、Q;③S△POQ=
| 2 | 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
(1)求椭圆C的轨迹方程;
(2)若A、B是椭圆C上的不同两点,弦AB(不平行于y轴)的垂直平分线与x轴相交于点M,则称弦AB是点M的一条“相关弦”,如果点M的坐标为M(
| 1 |
| 2 |
(3)根据解决问题(2)的经验与体会,请运用类比、推广等思想方法,提出一个与“相关弦”有关的具有研究价值的结论,并加以解决.(本小题将根据所提出问题的层次性给予不同的分值)
(08年黄冈中学二模)函数![]() 关于直线
关于直线![]() 对称的函数为
对称的函数为![]() ,又函数
,又函数![]() 的导函数为
的导函数为![]() ,记
,记![]()
(1)设曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,若
,若![]() 与圆
与圆![]() 相切,求
相切,求![]() 的值;
的值;
(2)求函数![]() 的单调区间;
的单调区间;
(3)求函数![]() 在[0,1]上的最大值;
在[0,1]上的最大值;
A.如果变量η与ξ之间存在着线性相关关系,则我们根据实验数据得到的点(xi,yi)(i=1,2, …,n)将散布在某一条直线的附近
B.如果两个变量η与ξ之间不存在着线性相关关系,那么根据它们的一组数据(xi,yi)(i=1,2, …,n)不能写出一个线性方程
C.设x,y是具有相关关系的两个变量,且x关于y的线性回归方程为![]() =bx+a,b叫做回归系数
=bx+a,b叫做回归系数
D.为使求出的线性回归方程有意义,可用统计假设检验的方法来判定变量η与ξ之间是否存在线性相关关系
查看习题详情和答案>>(本小题满分12分)
某市为了对学生的数理(数学与物理)学习能力进行分析,从10000名学生中随机抽出100位学生的数理综合学习能力等级分数(6分制)作为样本,分数频数分布如下表:
|
等级得分 |
|
|
|
|
|
|
|
人数 |
3 |
17 |
30 |
30 |
17 |
3 |
(Ⅰ)如果以能力等级分数大于4分作为良好的标准,从样本中任意抽取2名学生,求恰有1名学生为良好的概率;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值(例如区间 的中点值为1.5)作为代表:
的中点值为1.5)作为代表:
(ⅰ)据此,计算这100名学生数理学习能力等级分数的期望 及标准差
及标准差 (精确到0.1);
(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,估计该市这10000名学生中数理学习能力等级在 范围内的人数 .
范围内的人数 .
(Ⅲ)从这10000名学生中任意抽取5名同学,
他们数学与物理单科学习能力等级分
数如下表:


(ⅰ)请画出上表数据的散点图;
(ⅱ)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程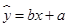 (附参考数据:
(附参考数据: )
)
查看习题详情和答案>>