摘要:知:-----8分 把x.y看作方程z2-11z+18=0的两根 解这个方程 得 z=2或z=9
网址:http://m.1010jiajiao.com/timu_id_8107[举报]
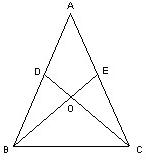 18、如图,已知AD=AE,∠ADC=∠AEB,BE和CD相交于O点,在不添加任何辅助线的情况下,请你写出由已知可得出的结论(例如,可得出△ABE≌△ACD,∠DOB=∠EOC,∠DOE=∠BOC.你写出的结论不能含有所举之例,要求写出4个)结论是
18、如图,已知AD=AE,∠ADC=∠AEB,BE和CD相交于O点,在不添加任何辅助线的情况下,请你写出由已知可得出的结论(例如,可得出△ABE≌△ACD,∠DOB=∠EOC,∠DOE=∠BOC.你写出的结论不能含有所举之例,要求写出4个)结论是①△DOB≌△EOC,②△BCD≌△CBE,③∠ABE=∠ACD,④BD=EC.
根据一元二次方程根的定义,解答下列问题.
一个三角形两边长分别为3cm和7cm,第三边长为a cm,且整数a满足a2-10a+21=0,求三角形的周长.
解:由已知可得4<a<10,则a可取5,6,7,8,9.(第一步)
当a=5时,代入a2-10a+21=52-10×5+21≠0,故a=5不是方程的根.
同理可知a=6,a=8,a=9都不是方程的根.
∴a=7是方程的根.(第二步)
∴△ABC的周长是3+7+7=17(cm).
上述过程中,第一步是根据
查看习题详情和答案>>
一个三角形两边长分别为3cm和7cm,第三边长为a cm,且整数a满足a2-10a+21=0,求三角形的周长.
解:由已知可得4<a<10,则a可取5,6,7,8,9.(第一步)
当a=5时,代入a2-10a+21=52-10×5+21≠0,故a=5不是方程的根.
同理可知a=6,a=8,a=9都不是方程的根.
∴a=7是方程的根.(第二步)
∴△ABC的周长是3+7+7=17(cm).
上述过程中,第一步是根据
三角形任意两边之和大于第三边,任意两边之差小于第三边
三角形任意两边之和大于第三边,任意两边之差小于第三边
,第二步应用了分类讨论
分类讨论
数学思想,确定a的值的大小是根据方程根的定义
方程根的定义
.7、A市和B市分别有某种库存机器12台和6台,现决定支援C村10台,D村8台,已知从A市调运一台机器到C村和D村的运费分别是400元和800元,从B市调运一台机器到C村和D村的运费分别是300元和500元.
(1)设B市运往C村机器x台,求总运费W关于x的函数关系式;
(2)若要求总运费不超过9000元,共有几种调运方案?
(3)求出总运费最低的调运方案,最低运费是多少元?
分析由已知条件填出下表:

查看习题详情和答案>>
(1)设B市运往C村机器x台,求总运费W关于x的函数关系式;
(2)若要求总运费不超过9000元,共有几种调运方案?
(3)求出总运费最低的调运方案,最低运费是多少元?
分析由已知条件填出下表:

为了顺应市场要求,某市电子玩具制造公司技术部研制开发一种新产品,年初上市后,公司经历了从亏损到盈利的过程.下面的二次函数图象(部分)刻画了该公司年初以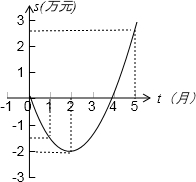 来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:
来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:
(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到6万元?
(3)求第9个月公司所获利润是多少万元? 查看习题详情和答案>>
 来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:
来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到6万元?
(3)求第9个月公司所获利润是多少万元? 查看习题详情和答案>>
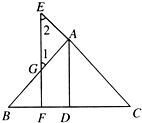 23、已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
23、已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.求证:AD平分∠BAC,填写分析和证明中的空白.
分析:要证明AD平分∠BAC,只要证明
∠BAD
=∠CAD
,而已知∠1=∠2,所以应联想这两个角分别和∠1、∠2的关系,由已知BC的两条垂线可推出
EF
∥AD
,这时再观察这两对角的关系已不难得到结论.证明:∵AD⊥BC,EF⊥BC(已知)
∴
EF
∥AD
(在同一平面内,垂直与同一直线的两直线平行
)∴
∠1
=∠BAD
(两直线平行,内错角相等),∠2
=∠CAD
(两直线平行,同位角相等)∵
∠1=∠2
(已知)∴
∠BAD=∠CAD
,即AD平分∠BAC(角平分线的定义
)