摘要：而于是故点P(x0,0)的所有“相关弦 的中点的横坐标都是x0-2.知.弦AB所在直线的方程是.代入中.整理得 (?)则是方程(?)的两个实根.且设点P的“相关弦 AB的弦长为l.则 因为0<<4xm=4(xm-2) =4x0-8,于是设t=,则t(0,4x0-8).
网址：http://m.1010jiajiao.com/timu_id_78599[举报]
已知函数f（x）=log
（x+1），当点P（x0，y0）在y=f（x）的图象上移动时，点Q（
，y0）（t∈R）在函数y=g（x）的图象上移动．
（1）若点P坐标为（1，-1），点Q也在y=f（x）的图象上，求t的值；
（2）求函数y=g（x）的解析式；
（3）当t＞0时，试探求一个函数h（x）使得f（x）+g（x）+h（x）在限定定义域为[0，1）时有最小值而没有最大值． 查看习题详情和答案>>
| 1 |
| 2 |
| x0-t+1 |
| 2 |
（1）若点P坐标为（1，-1），点Q也在y=f（x）的图象上，求t的值；
（2）求函数y=g（x）的解析式；
（3）当t＞0时，试探求一个函数h（x）使得f（x）+g（x）+h（x）在限定定义域为[0，1）时有最小值而没有最大值． 查看习题详情和答案>>
已知函数f（x）=log
（x+1），当点P（x0，y0）在y=f（x）的图象上移动时，点Q（
，y0）（t∈R）在函数y=g（x）的图象上移动．
（1）若点P坐标为（1，-1），点Q也在y=f（x）的图象上，求t的值；
（2）求函数y=g（x）的解析式；
（3）当t＞0时，试探求一个函数h（x）使得f（x）+g（x）+h（x）在限定定义域为[0，1）时有最小值而没有最大值．
查看习题详情和答案>>
| 1 |
| 2 |
| x0-t+1 |
| 2 |
（1）若点P坐标为（1，-1），点Q也在y=f（x）的图象上，求t的值；
（2）求函数y=g（x）的解析式；
（3）当t＞0时，试探求一个函数h（x）使得f（x）+g（x）+h（x）在限定定义域为[0，1）时有最小值而没有最大值．
（x+1），当点P（x0，y0）在y=f（x）的图象上移动时，点Q（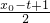
，y0）（t∈R）在函数y=g（x）的图象上移动．
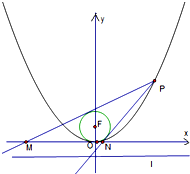已知抛物线C：x2=2py（p＞0）的焦点为