摘要:例5.已知椭圆的长.短轴端点分别为A.B.从此椭圆上一点M向x轴作垂线.恰好通过椭圆的左焦点.向量与是共线向量.(1)求椭圆的离心率e,(2)设Q是椭圆上任意一点. .分别是左.右焦点.求∠ 的取值范围,解:(1)∵.∴.∵是共线向量.∴.∴b=c,故.(2)设当且仅当时.cosθ=0.∴θ.说明:由于共线向量与解析几何中平行线.三点共线等具有异曲同工的作用.因此.解析几何中与平行线.三点共线等相关的问题均可在向量共线的新情景下设计问题.求解此类问题的关键是:正确理解向量共线与解析几何中平行.三点共线等的关系.把有关向量的问题转化为解析几何问题.
网址:http://m.1010jiajiao.com/timu_id_78037[举报]
已知椭圆![]() 的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点
的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点![]() ,向量
,向量![]() 与
与![]() 是共线向量。
是共线向量。
(1)求椭圆的离心率e;
(2)设Q是椭圆上任意一点, ![]() 、
、![]() 分别是左、右焦点,求∠
分别是左、右焦点,求∠![]() 的取值范围;
的取值范围;
已知椭圆 的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点
的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点 ,向量
,向量 与
与 是共线向量。
是共线向量。
(1)求椭圆的离心率e;
(2)设Q是椭圆上任意一点, 、
、 分别是左、右焦点,求∠
分别是左、右焦点,求∠ 的取值范围;
的取值范围;
 的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点
的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点 ,向量
,向量 与
与 是共线向量。
是共线向量。(1)求椭圆的离心率e;
(2)设Q是椭圆上任意一点,
 、
、 分别是左、右焦点,求∠
分别是左、右焦点,求∠ 的取值范围;
的取值范围;已知椭圆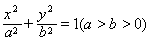 的左、右焦点分别为
的左、右焦点分别为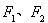 ,且
,且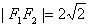 ,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.
,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.
(1)求椭圆方程;
(2)设椭圆与直线 相交于不同的两点M、N,又点
相交于不同的两点M、N,又点 ,当
,当 时,求实数m的取值范围,
时,求实数m的取值范围,
查看习题详情和答案>>
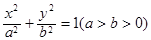 的左、右焦点分别为
的左、右焦点分别为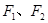 ,且
,且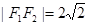 ,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.
,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.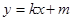 相交于不同的两点M、N,又点
相交于不同的两点M、N,又点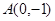 ,当
,当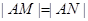 时,求实数m的取值范围,
时,求实数m的取值范围,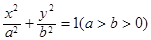 的左、右焦点分别为
的左、右焦点分别为 ,且
,且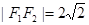 ,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.
,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.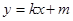 相交于不同的两点M、N,又点
相交于不同的两点M、N,又点 ,当
,当 时,求实数m的取值范围,
时,求实数m的取值范围,