摘要：例3. 已知⊙M:轴上的动点.QA.QB分别切⊙M于A.B两点.(1)如果.求直线MQ的方程, (2)求动弦AB的中点P的轨迹方程. 解:(1)由.可得由射影定理.得 在Rt△MOQ中. 故. 所以直线AB方程是 (2)连接MB.MQ.设由点M.P.Q在一直线上.得由射影定理得即 把消去a.并注意到.可得说明:适时应用平面几何知识.这是快速解答本题的要害所在.
网址：http://m.1010jiajiao.com/timu_id_78035[举报]
，求直线MQ的方程；已知圆M：x2+（y-2）2=1，Q是x轴上的动点，QA、QB分别切圆M于A，B两点．
（1）若点Q的坐标为（1，0），求切线QA、QB的方程；
（2）求四边形QAMB的面积的最小值；
（3）若|AB|=
，求直线MQ的方程．
查看习题详情和答案>>
（1）若点Q的坐标为（1，0），求切线QA、QB的方程；
（2）求四边形QAMB的面积的最小值；
（3）若|AB|=
4
| ||
| 3 |
已知圆M：x2+（y-2）2=1，Q是x轴上的动点，QA、QB分别切圆M于A，B两点
（1）求四边形QAMB的面积的最小值
（2）若点Q的坐标为（1，0），求切线QA、QB及直线AB的方程．
查看习题详情和答案>>
（1）求四边形QAMB的面积的最小值
（2）若点Q的坐标为（1，0），求切线QA、QB及直线AB的方程．
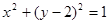,Q是x轴上的动点，QA、QB分别切圆M于A、B两点。
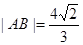，求
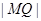的长；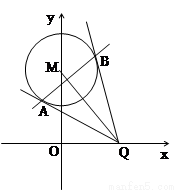
(2)求证：直线AB恒过定点，并求出定点坐标．