题目内容
已知⊙M：x2+(y-2)2=1,Q是x轴上的动点，QA、QB分别切⊙M于A、B两点.（1）若|AB|=
，求直线MQ的方程；
（2）求证：直线AB恒过定点，并求出此定点坐标.
(1)解析：设AB交MQ于E点，(如下图)则易知MQ垂直平分线段AB，
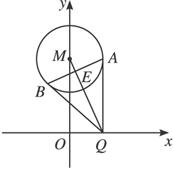
∴|ME|=
.
由射影定理知，|MA|2=|ME|·|MQ|，
∴|MQ|=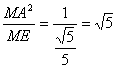
.
M（0，2），设Q（a,0）,
则|MQ|=
.
解得a=±1,即Q（1，0）或Q（-1，0）.
∴直线MQ的方程为2x+y-2=0或2x-y+2=0.
(2)证明：QA、QB是⊙M的切线，则MA⊥AQ，MB⊥BQ，故A、M、B、Q四点共圆且MQ是此圆直径，设此圆圆心为F.设Q（a,0）,则F（
,1）,|MQ|=
,∴⊙F的方程为即（x-
）2+(y-1)2=
即x2+y2-ax-2y=0联立x2+(y-2)2=1，消去x2+y2项，即得两圆公共弦AB所在直线的方程：-ax+2y-3=0.
故直线AB恒过定点（0，
）.
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
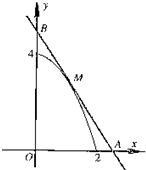如图，已知M是函数y=4-x2（1＜x＜2）的图象C上一点，过M点作曲线C的切线与x轴、y轴分别交于点A，B，O是坐标原点，求△AOB面积的最小值．已知M={(x，y)|y=
，y≠0}，N={（x，y）|y=x+b}，若M∩N≠∅，则b∈（ ）
| 9-x2 |
A、[-3
| ||||
B、(-3
| ||||
C、(-3，3
| ||||
D、[-3，3
|