题目内容
已知:⊙M的方程为x2+(y-2)2=1,Q点是x轴上的动点,QA、QB分别切⊙M于A、B.
(1)求弦AB中点P的轨迹方程;
(2)若|AB|>
,求点Q的横坐标xQ的取值范围.
(1)求弦AB中点P的轨迹方程;
(2)若|AB|>
4
| ||
| 3 |
分析:(1)利用圆切线的性质得到M、P、Q三点共线,MA⊥AQ于P;利用直角三角形的射影定理得到P,Q的坐标间的关系;利用三点关系
得到P,Q的另一个等式,两式联立,消去Q的坐标,得到P的轨迹方程.
(2)利用直角三角形的勾股定理将AP用MP的长不是,利用两点距离公式将AP长用p的坐标表示,进一步用Q的坐标表示,列出不等式求出Q的坐标的取值范围.
得到P,Q的另一个等式,两式联立,消去Q的坐标,得到P的轨迹方程.
(2)利用直角三角形的勾股定理将AP用MP的长不是,利用两点距离公式将AP长用p的坐标表示,进一步用Q的坐标表示,列出不等式求出Q的坐标的取值范围.
解答: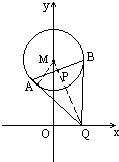 解:(1)连接MA、MQ,则M、P、Q三点共线,MA⊥AQ于P.
解:(1)连接MA、MQ,则M、P、Q三点共线,MA⊥AQ于P.
设P(x,y),其中-1<x<1,1<y<2,Q(xQ,0)∵|AM|2=|MP|•|MQ|
•
=1
∴
•
=1①
又当x0≠0时,∵KMP=KMO
∴
=
即xQ=
②
将②式代入①式得:[x2+(y-2)2]•[
+4]=1[x2+(y-2)2]•
=
[x2+(y-2)2]2=
(y-2)2x2+(y-2)2=
∵y<2x2+(y-2)2=
(2-y)
即x2+y2-
y+3=0,即x2+(y-
y)2=
∵xQ≠0,
∴x≠0
又当xQ=0时,由②知x=0代入①得|y-2|=
,
解得y=
将(0,
)代入x2+(y-
)2=
满足方程,
所以(0,
)在所求轨迹上,
所以x2+(y-
)2=
(y≠2)为所求的轨迹方程.
(2)∵|AB|>
,
∴|AP|=
|AB|>
|AP|2=|MA|2-|MP|2=1-|MP|2>
1-[(2-y)2+x2]>
x2+(2-y)2<
由(1)得
>
xQ2+4>9,xQ2>5
∴xQ>
或xQ<-
 解:(1)连接MA、MQ,则M、P、Q三点共线,MA⊥AQ于P.
解:(1)连接MA、MQ,则M、P、Q三点共线,MA⊥AQ于P.设P(x,y),其中-1<x<1,1<y<2,Q(xQ,0)∵|AM|2=|MP|•|MQ|
| (x-0)2+(y-2)2 |
| (xQ-0)2+(0-2)2 |
∴
| x2+(y-2)2 |
(
|
又当x0≠0时,∵KMP=KMO
∴
| y-2 |
| x-0 |
| 0-2 |
| xQ-0 |
| -2x |
| y-2 |
将②式代入①式得:[x2+(y-2)2]•[
| 4x2 |
| (y-2)2 |
| x2+(y-2)2 |
| (y-2)2 |
| 1 |
| 4 |
| 1 |
| 4 |
| |y-2| |
| 2 |
∵y<2x2+(y-2)2=
| 1 |
| 2 |
即x2+y2-
| 7 |
| 2 |
| 7 |
| 4 |
| 1 |
| 16 |
∵xQ≠0,
∴x≠0
又当xQ=0时,由②知x=0代入①得|y-2|=
| 1 |
| 2 |
解得y=
| 3 |
| 2 |
| 3 |
| 2 |
| 7 |
| 4 |
| 1 |
| 16 |
所以(0,
| 3 |
| 2 |
所以x2+(y-
| 7 |
| 4 |
| 1 |
| 16 |
(2)∵|AB|>
4
| ||
| 3 |
∴|AP|=
| 1 |
| 2 |
2
| ||
| 3 |
|AP|2=|MA|2-|MP|2=1-|MP|2>
| 8 |
| 9 |
| 8 |
| 9 |
| 1 |
| 9 |
由(1)得
| 1 | ||
|
| 1 |
| 9 |
∴xQ>
| 5 |
| 5 |
点评:本题考查过圆外一点做圆的两条切线,圆心与该点的连线垂直平分两切点连线;直角三角形的射影定理;直角三角形的勾股定理.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点.
已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点.