摘要：5．重视应用在历年的高考试题中.经常出现解析几何的应用题.如01年的天津理科试题.03年的上海文理科试题.03年全国文科旧课程卷试题.03年的广东试题及江苏的线性规划题等.都是有关解析几何的应用题． 例11某中心接到其正东.正西.正北方向三个观测点的报告:正西.正北两个观测点同时听到了一声巨响.正东观测点听到的时间比其他两观测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上) 解:如图.以接报中心为原点O.正东.正北方向为x轴.y轴正向.建立直角坐标系.设A.B.C分别是西.东.北观测点.则A.C设P(x,y)为巨响为生点.由A.C同时听到巨响声.得|PA|=|PB|.故P在AC的垂直平分线PO上.PO的方程为y=-x.因B点比A点晚4s听到爆炸声.故|PB|- |PA|=340×4=1360由双曲线定义知P点在以A.B为焦点的双曲线上.依题意得a=680, c=1020.用y=-x代入上式.得.∵|PB|>|PA|, 答:巨响发生在接报中心的西偏北450距中心处.(二)05年高考预测
网址：http://m.1010jiajiao.com/timu_id_78025[举报]
某校在2011年高考报名中有男生800人、女生600人，现要从中抽取一个容量为35的样本，则男生、女生抽取的人数分别为（ ）
| A、20，15 | B、22，13 | C、25，10 | D、26，9 |
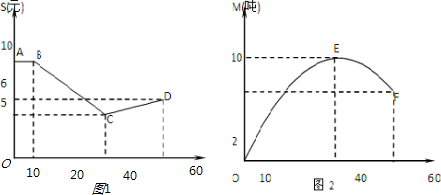
（2013•湖南）某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横直线的交叉点以及三角形顶点）处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收获Y（单位：kg）与它的“相近”作物株数X之间的关系如下表所示：| X | 1 | 2 | 3 | 4 |
| Y | 51 | 48 | 45 | 42 |
（I）从三角形地块的内部和边界上分别随机选取一株作物，求它们恰 好“相近”的概率；
（II）在所种作物中随机选取一株，求它的年收获量的分布列与数学期望．
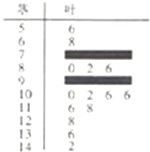某数学老师对本校2013届高三学生的高考数学成绩按1：200进行分层抽样抽取了20名学生的成绩，并用茎叶图记录分数如图所示，但部分数据不小心丢失，同时得到如下所示的频率分布表：| 分数段（分） | [50，70） | [70，90） | [90，110） | [110，130） | [130，150） | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
（2）从成绩在[100，130）范围内的学生中随机选4人，设其中成绩在[100，110）内的人数为X，求X的分布列及数学期望．
