摘要：∴A1C⊥平面BDC1.(Ⅱ)取EF的中点H.连结BH.CH.又E.F分别是AC.B1C的中点.解法二:(Ⅰ)以点C为坐标原点建立如图所示的空间直角坐标系,则C.D,A1,C1,D1 可证.BD1⊥平面AB1C.
网址：http://m.1010jiajiao.com/timu_id_78009[举报]
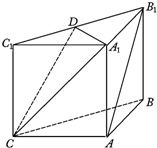如图，在三棱柱ABC-A1B1C1中，侧面ABB1A1，ACC1A1均为正方形，∠BAC=90°，点D是棱B1C1的中点．（Ⅰ）求证：A1D⊥平面BB1C1C；（Ⅱ）求二面角D-A1C-A的余弦值．
（文科）如图甲，
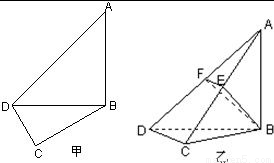
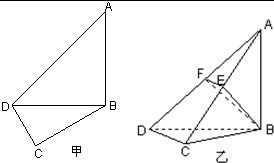在平面四边形ABCD中，已知∠A=45°，∠C=90°，∠ADC=105°，AB=BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．（Ⅰ）求证：DC⊥平面ABC；
（Ⅱ）设CD=a，求三棱锥A-BFE的体积． 查看习题详情和答案>>
如图，在三棱柱ABC-A1B1C1中，侧面ABB1A1，ACC1A1均为正方形，∠BAC=90°，点D是棱B1C1的中点．
（Ⅰ）求证：A1D⊥平面BB1C1C；（Ⅱ）求二面角D-A1C-A的余弦值．
（文科）如图甲，在平面四边形ABCD中，已知∠A=45°，∠C=90°，∠ADC=105°，AB=BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．
（Ⅰ）求证：DC⊥平面ABC；
（Ⅱ）设CD=a，求三棱锥A-BFE的体积．
如图，在三棱柱ABC-A1B1C1中，侧面ABB1A1，ACC1A1均为正方形，∠BAC=90°，点D是棱B1C1的中点．
（Ⅰ）求证：A1D⊥平面BB1C1C；（Ⅱ）求二面角D-A1C-A的余弦值．
（文科）如图甲，在平面四边形ABCD中，已知∠A=45°，∠C=90°，∠ADC=105°，AB=BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．
（Ⅰ）求证：DC⊥平面ABC；
（Ⅱ）设CD=a，求三棱锥A-BFE的体积．
查看习题详情和答案>>
（Ⅰ）求证：A1D⊥平面BB1C1C；（Ⅱ）求二面角D-A1C-A的余弦值．
（文科）如图甲，在平面四边形ABCD中，已知∠A=45°，∠C=90°，∠ADC=105°，AB=BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．
（Ⅰ）求证：DC⊥平面ABC；
（Ⅱ）设CD=a，求三棱锥A-BFE的体积．
查看习题详情和答案>>
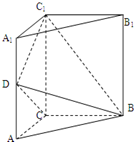（2014•江门模拟）如图，三棱柱ABC-A1B1C1中，侧棱垂直底面，AC⊥BC，D是棱AA1的中点，AA1=2AC=2BC=2a（a＞0）．
（2005•朝阳区一模）直三棱柱ABC-A1B1C1中，AB⊥BC，E是A1C的中点，ED⊥A1C且交AC于D，A1A=AB=