题目内容
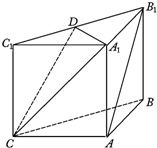 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.(Ⅰ)求证:A1D⊥平面BB1C1C;(Ⅱ)求二面角D-A1C-A的余弦值.
(文科)如图甲,
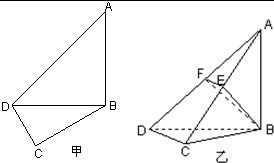 在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.(Ⅰ)求证:DC⊥平面ABC;
(Ⅱ)设CD=a,求三棱锥A-BFE的体积.
分析:(Ⅰ) 先证明三棱柱是直三棱柱,由CC1⊥A1D,A1D⊥B1C1,证得A1D⊥平面BB1C1C.
(Ⅱ) 如图所示建立直角坐标系A-xyz,求出二面角的两个面的法向量,求出两个法向量夹角的
余弦值,此余弦值的相反数即为所求.
(文答案)(Ⅰ) AB⊥BD,由面面垂直的性质可得AB⊥底面BDC,故AB⊥CD,又DC⊥BC,DC⊥平面ABC.
(Ⅱ) 证得EF⊥平面ABC,可得VA-BFE=VF-AEB=
S△AEB•FE,求出三角形AEB的面积和EF的长度,
即可求得结果.
(Ⅱ) 如图所示建立直角坐标系A-xyz,求出二面角的两个面的法向量,求出两个法向量夹角的
余弦值,此余弦值的相反数即为所求.
(文答案)(Ⅰ) AB⊥BD,由面面垂直的性质可得AB⊥底面BDC,故AB⊥CD,又DC⊥BC,DC⊥平面ABC.
(Ⅱ) 证得EF⊥平面ABC,可得VA-BFE=VF-AEB=
| 1 |
| 3 |
即可求得结果.
解答: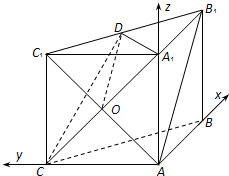 (Ⅰ)证明:因为侧面ABB1A1,ACC1A1均为正方形,
(Ⅰ)证明:因为侧面ABB1A1,ACC1A1均为正方形,
所以AA1⊥AC,AA1⊥AB,
所以AA1⊥平面ABC,三棱柱ABC-A1B1C1是直三棱柱.
因为A1D?平面A1B1C1,所以CC1⊥A1D,
又因为A1B1=A1C1,D为B1C1中点,所以A1D⊥B1C1.
因为CC1∩B1C1=C1,所以A1D⊥平面BB1C1C.
(Ⅱ)解:因为侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,
所以AB,AC,AA1两两互相垂直,如图所示建立直角坐标系A-xyz.
设AB=1,则C(0,1,0), B(1,0,0), A1(0,0,1), D(
,
,1).
=(
,
,0),
=(0,1,-1),设平面A1DC的法向量为
=(x,y,z),
则有
,
,x=-y=-z,取x=1,得
=(1,-1,-1).
又因为|
|=
=
,AB⊥平面ACC1A1,
所以平面ACC1A1的法向量为
=(1,0,0),因为二面角D-A1C-A是钝角,
所以,二面角D-A1C-A的余弦值为-
.
(文答案)(Ⅰ)证明:在图甲中∵AB=BD且∠A=45°∴∠ADB=45°,∠ABD=90°,即AB⊥BD.
在图乙中,∵平面ABD⊥平面BDC,且平面ABD∩平面BDC=BD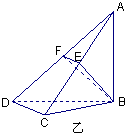 ,∴AB⊥底面BDC,∴AB⊥CD.
,∴AB⊥底面BDC,∴AB⊥CD.
又∠DCB=90°,∴DC⊥BC,且AB∩BC=B,∴DC⊥平面ABC.
(Ⅱ)解:∵E、F分别为AC、AD的中点,∴EF∥CD,又由(Ⅰ)知,DC⊥平面ABC,
∴EF⊥平面ABC,∴VA-BFE=VF-AEB=
S△AEB•FE.
在图甲中,∵∠ADC=105°,∴∠BDC=60°,∠DBC=30°,
由CD=a得BD=2a,BC=
a,EF=
CD=
a,
∴S△ABC=
AB•BC=
•2a•
a=
a2,∴S△AEB=
a2,
∴VA-BFE=
•
a2•
a=
a3.
 (Ⅰ)证明:因为侧面ABB1A1,ACC1A1均为正方形,
(Ⅰ)证明:因为侧面ABB1A1,ACC1A1均为正方形,所以AA1⊥AC,AA1⊥AB,
所以AA1⊥平面ABC,三棱柱ABC-A1B1C1是直三棱柱.
因为A1D?平面A1B1C1,所以CC1⊥A1D,
又因为A1B1=A1C1,D为B1C1中点,所以A1D⊥B1C1.
因为CC1∩B1C1=C1,所以A1D⊥平面BB1C1C.
(Ⅱ)解:因为侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,
所以AB,AC,AA1两两互相垂直,如图所示建立直角坐标系A-xyz.
设AB=1,则C(0,1,0), B(1,0,0), A1(0,0,1), D(
| 1 |
| 2 |
| 1 |
| 2 |
| A1D |
| 1 |
| 2 |
| 1 |
| 2 |
| A1C |
| n |
则有
|
|
| n |
又因为|
| ||||
|
|
| 1 | ||
|
| ||
| 3 |
所以平面ACC1A1的法向量为
| AB |
所以,二面角D-A1C-A的余弦值为-
| ||
| 3 |
(文答案)(Ⅰ)证明:在图甲中∵AB=BD且∠A=45°∴∠ADB=45°,∠ABD=90°,即AB⊥BD.
在图乙中,∵平面ABD⊥平面BDC,且平面ABD∩平面BDC=BD
 ,∴AB⊥底面BDC,∴AB⊥CD.
,∴AB⊥底面BDC,∴AB⊥CD.又∠DCB=90°,∴DC⊥BC,且AB∩BC=B,∴DC⊥平面ABC.
(Ⅱ)解:∵E、F分别为AC、AD的中点,∴EF∥CD,又由(Ⅰ)知,DC⊥平面ABC,
∴EF⊥平面ABC,∴VA-BFE=VF-AEB=
| 1 |
| 3 |
在图甲中,∵∠ADC=105°,∴∠BDC=60°,∠DBC=30°,
由CD=a得BD=2a,BC=
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
∴VA-BFE=
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 12 |
点评:本题考查证明线线垂直、线面垂直的方法,求棱锥的体积,二面角的大小,直线与平面垂直的判定、性质的应用.

练习册系列答案
相关题目
 如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )
如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )| A、3:2 | B、7:5 | C、8:5 | D、9:5 |
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,A1A=AC=2,BC=1,AB=
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,A1A=AC=2,BC=1,AB= 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3 (2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2
(2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2 如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.
如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.