摘要:线段AP的长 ∠AOP的弧度数 大圆劣弧AP的长8.球的表面积及体积公式 S球表=4πR2 V球=πR3⑴球的体积公式可以这样来考虑:我们把球面分成若干个边是曲线的小“曲边三角形 ,以球心为顶点.以这些小曲边三角形的顶点为底面三角形的顶点.得到若干个小三棱锥.所有这些小三棱锥的体积和可以看作是球体积的近似值.当小三棱锥的个数无限增加.且所有这些小三棱锥的底面积无限变小时.小三棱锥的体积和就变成球体积.同时小三棱锥底面面积的和就变成球面面积,小三棱锥高变成球半径.由于第n个小三棱锥的体积=Snhn(Sn为该小三棱锥的底面积,hn为小三棱锥高).所以V球=S球面?R=?4πR2?R=πR3. ⑵球与其它几何体的切接问题.要仔细观察.分析.弄清相关元素的位置关系和数量关系.选择最佳角度作出截面.以使空间问题平面化.
网址:http://m.1010jiajiao.com/timu_id_78000[举报]
在△ABC中,a,b,C分别是内角A,B,C所对的边,并且sinA=2sinBcosC,a=b=2
.
(1)求∠A的值;
(2)若点P为线段AB上一点,且
•
=12,求线段AP的长.
查看习题详情和答案>>
| 5 |
(1)求∠A的值;
(2)若点P为线段AB上一点,且
| CA |
| CP |
 在长方体ABCD-A1B1C1D1中,AA1=AD=2,点E在棱CD上,且CE=
在长方体ABCD-A1B1C1D1中,AA1=AD=2,点E在棱CD上,且CE=| 1 |
| 3 |
(1)求证:AD1⊥平面A1B1D;
(2)在棱AA1上是否存在点P,使DP∥平面B1AE?若存在,求出线段AP的长;若不存在,请说明理由;
(3)若二面角A-B1E-A1的余弦值为
| ||
| 6 |
 如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P.
如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P. 在长方体ABCD-A1B1C1D1中,AA1=AD=2,E是棱CD上的一点.
在长方体ABCD-A1B1C1D1中,AA1=AD=2,E是棱CD上的一点.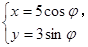 (
(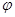 是参数)的左焦点,P是椭圆上对应于
是参数)的左焦点,P是椭圆上对应于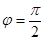 的点,那么线段AP的长是
的点,那么线段AP的长是