题目内容
在△ABC中,a,b,C分别是内角A,B,C所对的边,并且sinA=2sinBcosC,a=b=2
.
(1)求∠A的值;
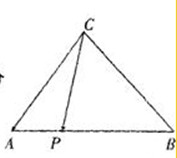
(2)若点P为线段AB上一点,且
•
=12,求线段AP的长.
| 5 |
(1)求∠A的值;
(2)若点P为线段AB上一点,且
| CA |
| CP |
分析:(1)利用三角形的内角和以及诱导公式、两角和的正弦函数化简sinA=2sinBcosC,推出sin(B-C)=0,然后求出三角形的形状,求出∠A的值.
(2)求出
,利用
•
,直接展开,即可求出线段AP的长.
(2)求出
| CP |
| CA |
| CP |
解答:解:(1)∵sinA=sin[180°-(B+C)]=sin(B+C)=sinBcosC+cosBsinC=2sinBcosC,
∴cosBsinC=sinBcosC,
sinBcosC-cosBsinC=sin(B-C)=0,
∴∠B-∠C=0或180°,
∵∠B,∠C是三角形的内角,∴∠B-∠C=0
∴∠B=∠C,
即b=c,
又a=b=2
,
∴a=b=c,
三角形是等边三角形,
∴∠A=60°.
(2)∵
=
+
,
•
=12,
∴(
+
) •
=12
∴
2+
•
=12,
∴|
|2+|
| • |
| cos120°=12,
即(2
)2+ |
| •2
•(-
) =12,
整理得|
| =
.
∴cosBsinC=sinBcosC,
sinBcosC-cosBsinC=sin(B-C)=0,
∴∠B-∠C=0或180°,
∵∠B,∠C是三角形的内角,∴∠B-∠C=0
∴∠B=∠C,
即b=c,
又a=b=2
| 5 |
∴a=b=c,
三角形是等边三角形,
∴∠A=60°.
(2)∵
| CP |
| CA |
| AP |
| CA |
| CP |
∴(
| CA |
| AP |
| CA |
∴
| CA |
| AP |
| CA |
∴|
| CA |
| AP |
| CA |
即(2
| 5 |
| AP |
| 5 |
| 1 |
| 2 |
整理得|
| AP |
8
| ||
| 5 |

点评:本题是中档题,考查三角函数的化简求值,两角和与差的三角函数,三角方程的解法,向量的数量积,注意向量的夹角与向量的关系,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|