题目内容
 在长方体ABCD-A1B1C1D1中,AA1=AD=2,点E在棱CD上,且CE=
在长方体ABCD-A1B1C1D1中,AA1=AD=2,点E在棱CD上,且CE=| 1 |
| 3 |
(1)求证:AD1⊥平面A1B1D;
(2)在棱AA1上是否存在点P,使DP∥平面B1AE?若存在,求出线段AP的长;若不存在,请说明理由;
(3)若二面角A-B1E-A1的余弦值为
| ||
| 6 |
分析:(1)利用长方体和正方体的性质、线面垂直的判定定理即可证明;
(2)通过建立空间直角坐标系,若DP∥平面AB1E,设
为平面AB1E的法向量?
•
=0,且
?平面AB1E,求出即可;
(3)利用(1)(2)的结论即可得到此二面角的两个面的法向量,进而利用法向量的夹角即可得到二面角的余弦值,解出即可.
(2)通过建立空间直角坐标系,若DP∥平面AB1E,设
| n |
| DP |
| n |
| DP |
(3)利用(1)(2)的结论即可得到此二面角的两个面的法向量,进而利用法向量的夹角即可得到二面角的余弦值,解出即可.
解答:(1)证明:在长方体ABCD-A1B1C1D1中,∵A1B1⊥面A1D1DA,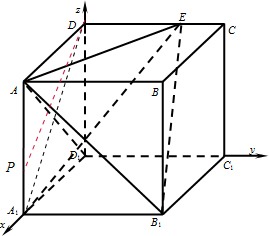
∴A1B1⊥AD1.
在矩形A1D1DA中,∵AA1=AD=2,
∴AD1⊥A1D.
又A1D∩A1B1=A1,
∴AD1⊥平面A1B1D.
(2)如图,在长方体ABCD-A1B1C1D1中,以D1为原点建立空间直角坐标系D1-xyz.
依题意可知,D1(0,0,0),A1(2,0,0),D(0,0,2),A(2,0,2),
设AB的长为x,则C1(0,x,0),B1(2,x,0),C(0,x,2),E(0,
x,2).
假设在棱AA1上存在点P,使得DP∥平面B1AE.
设点P(2,0,y),则
=(2,0,y-2),
=(0,0,y-2).
易知
=(-2,-
x,2),
=(-2,
x,0).
设平面B1AE的一个法向量为n=(a,b,c),
则
,即
.
令b=3得,a=x,c=
x,∴
=(x,3,
x).
∵DP∥平面B1AE,∴
•
=0且DP?平面B1AE.
得2x+(y-2)•
x=0,∴y=
.
∴
=(0,0,-
),|
|=
,
∴AP的长为
.
(3)∵CD∥A1B1,且点E∈CD,
∴平面A1B1E、平面A1B1D与面A1B1CD是同一个平面.
由(1)可知,AD1⊥面A1B1D,
∴
=(2,0,2)是平面A1B1E的一个法向量.
由(2)可知,平面B1AE的一个法向量为n=(x,3,
x).
∵二面角A-B1E-A1的余弦值为
,
∴cosθ=
=
=
,解得x=3
.
故AB的长为3
.

∴A1B1⊥AD1.
在矩形A1D1DA中,∵AA1=AD=2,
∴AD1⊥A1D.
又A1D∩A1B1=A1,
∴AD1⊥平面A1B1D.
(2)如图,在长方体ABCD-A1B1C1D1中,以D1为原点建立空间直角坐标系D1-xyz.
依题意可知,D1(0,0,0),A1(2,0,0),D(0,0,2),A(2,0,2),
设AB的长为x,则C1(0,x,0),B1(2,x,0),C(0,x,2),E(0,
| 2 |
| 3 |
假设在棱AA1上存在点P,使得DP∥平面B1AE.
设点P(2,0,y),则
| DP |
| AP |
易知
| B1E |
| 1 |
| 3 |
| AE |
| 2 |
| 3 |
设平面B1AE的一个法向量为n=(a,b,c),
则
|
|
令b=3得,a=x,c=
| 3 |
| 2 |
| n |
| 3 |
| 2 |
∵DP∥平面B1AE,∴
| DP |
| n |
得2x+(y-2)•
| 3 |
| 2 |
| 2 |
| 3 |
∴
| AP |
| 4 |
| 3 |
| AP |
| 4 |
| 3 |
∴AP的长为
| 4 |
| 3 |
(3)∵CD∥A1B1,且点E∈CD,
∴平面A1B1E、平面A1B1D与面A1B1CD是同一个平面.
由(1)可知,AD1⊥面A1B1D,
∴
| D1A |
由(2)可知,平面B1AE的一个法向量为n=(x,3,
| 3 |
| 2 |
∵二面角A-B1E-A1的余弦值为
| ||
| 6 |
∴cosθ=
| ||
| 6 |
|
| ||||
|
|
| |2x+3x| | ||||||
2
|
| 2 |
故AB的长为3
| 2 |
点评:熟练掌握长方体和正方体的性质、线面垂直的判定定理、通过建立空间直角坐标系的方法求出平面的法向量并利用法向量及其数量积即可求出线面角、二面角是解题的关键.

练习册系列答案
相关题目
 在长方体ABCD-A'B'C'D'中,AB=
在长方体ABCD-A'B'C'D'中,AB= 如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比.
如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比. (2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.
(2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离. (2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.
(2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1. 已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.
已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.