摘要: 已知椭圆的中心在原点.集点在坐标轴上.焦距为.另一双曲线与此椭圆有公共焦点.且其实轴比椭圆的长轴小8.两曲线的离心率之比为3:7.求此椭圆.双曲线的方程.
网址:http://m.1010jiajiao.com/timu_id_77825[举报]
下图展示了一个由区间 (其中
(其中 为一正实数)到实数集R上的映射过程:区间
为一正实数)到实数集R上的映射过程:区间 中的实数
中的实数 对应线段
对应线段 上的点
上的点 ,如图1;将线段
,如图1;将线段 围成一个离心率为
围成一个离心率为 的椭圆,使两端点
的椭圆,使两端点 、
、 恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在
恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在 轴上,已知此时点
轴上,已知此时点 的坐标为
的坐标为 ,如图3,在图形变化过程中,图1中线段
,如图3,在图形变化过程中,图1中线段 的长度对应于图3中的椭圆弧ADM的长度.图3中直线
的长度对应于图3中的椭圆弧ADM的长度.图3中直线 与直线
与直线 交于点
交于点 ,则与实数
,则与实数 对应的实数就是
对应的实数就是 ,记作
,记作 ,
,

现给出下列5个命题
① ;
②函数
;
②函数 是奇函数;③函数
是奇函数;③函数 在
在 上单调递增; ④.函数
上单调递增; ④.函数 的图象关于点
的图象关于点 对称;⑤函数
对称;⑤函数 时AM过椭圆的右焦点.其中所有的真命题是: ( )
时AM过椭圆的右焦点.其中所有的真命题是: ( )
A.①③⑤ B.②③④ C.②③⑤ D.③④⑤
查看习题详情和答案>>
下图展示了一个由区间 (其中
(其中 为一正实数)到实数集R上的映射过程:区间
为一正实数)到实数集R上的映射过程:区间 中的实数
中的实数 对应线段
对应线段 上的点
上的点 ,如图1;将线段
,如图1;将线段 围成一个离心率为
围成一个离心率为 的椭圆,使两端点
的椭圆,使两端点 、
、 恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在
恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在 轴上,已知此时点
轴上,已知此时点 的坐标为
的坐标为 ,如图3,在图形变化过程中,图1中线段
,如图3,在图形变化过程中,图1中线段 的长度对应于图3中的椭圆弧ADM的长度.图3中直线
的长度对应于图3中的椭圆弧ADM的长度.图3中直线 与直线
与直线 交于点
交于点 ,则与实数
,则与实数 对应的实数就是
对应的实数就是 ,记作
,记作 ,
,
现给出下列5个命题
① ; ②函数
; ②函数 是奇函数;③函数
是奇函数;③函数 在
在 上单调递增; ④.函数
上单调递增; ④.函数 的图象关于点
的图象关于点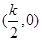 对称;⑤函数
对称;⑤函数 时AM过椭圆的右焦点.其中所有的真命题是: ( )
时AM过椭圆的右焦点.其中所有的真命题是: ( )
| A.①③⑤ | B.②③④ | C.②③⑤ | D.③④⑤ |
下图展示了一个由区间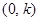 (其中
(其中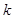 为一正实数)到实数集R上的映射过程:区间
为一正实数)到实数集R上的映射过程:区间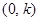 中的实数
中的实数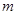 对应线段
对应线段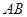 上的点
上的点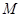 ,如图1;将线段
,如图1;将线段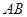 围成一个离心率为
围成一个离心率为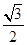 的椭圆,使两端点
的椭圆,使两端点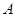 、
、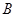 恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在
恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在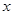 轴上,已知此时点
轴上,已知此时点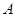 的坐标为
的坐标为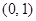 ,如图3,在图形变化过程中,图1中线段
,如图3,在图形变化过程中,图1中线段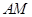 的长度对应于图3中的椭圆弧ADM的长度.图3中直线
的长度对应于图3中的椭圆弧ADM的长度.图3中直线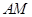 与直线
与直线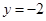 交于点
交于点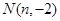 ,则与实数
,则与实数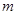 对应的实数就是
对应的实数就是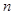 ,记作
,记作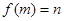 ,
,
现给出下列5个命题
①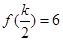 ; ②函数
; ②函数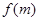 是奇函数;③函数
是奇函数;③函数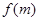 在
在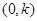 上单调递增; ④.函数
上单调递增; ④.函数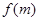 的图象关于点
的图象关于点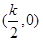 对称;⑤函数
对称;⑤函数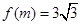 时AM过椭圆的右焦点.其中所有的真命题是: ( )
时AM过椭圆的右焦点.其中所有的真命题是: ( )
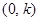 (其中
(其中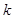 为一正实数)到实数集R上的映射过程:区间
为一正实数)到实数集R上的映射过程:区间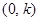 中的实数
中的实数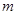 对应线段
对应线段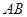 上的点
上的点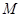 ,如图1;将线段
,如图1;将线段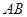 围成一个离心率为
围成一个离心率为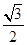 的椭圆,使两端点
的椭圆,使两端点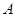 、
、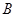 恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在
恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在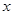 轴上,已知此时点
轴上,已知此时点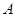 的坐标为
的坐标为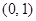 ,如图3,在图形变化过程中,图1中线段
,如图3,在图形变化过程中,图1中线段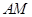 的长度对应于图3中的椭圆弧ADM的长度.图3中直线
的长度对应于图3中的椭圆弧ADM的长度.图3中直线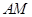 与直线
与直线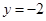 交于点
交于点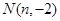 ,则与实数
,则与实数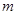 对应的实数就是
对应的实数就是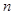 ,记作
,记作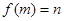 ,
,
现给出下列5个命题
①
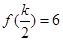 ; ②函数
; ②函数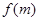 是奇函数;③函数
是奇函数;③函数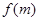 在
在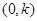 上单调递增; ④.函数
上单调递增; ④.函数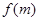 的图象关于点
的图象关于点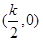 对称;⑤函数
对称;⑤函数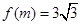 时AM过椭圆的右焦点.其中所有的真命题是: ( )
时AM过椭圆的右焦点.其中所有的真命题是: ( )| A.①③⑤ | B.②③④ | C.②③⑤ | D.③④⑤ |
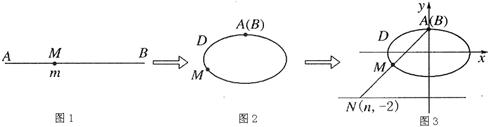
如图展示了一个由区间(0,k)(其中k为一正实数)到实数集R上的映射过程:区间(0,k)中的实数m对应线段AB上的点M,如图1;将线段AB围成一个离心率为 的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,

现给出下列5个命题① ;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点
;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点 对称;⑤函数
对称;⑤函数 时AM过椭圆的右焦点.其中所有的真命题是( )
时AM过椭圆的右焦点.其中所有的真命题是( )
A.①③⑤
B.②③④
C.②③⑤
D.③④⑤
查看习题详情和答案>>
 的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
现给出下列5个命题①
 ;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点
;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点 对称;⑤函数
对称;⑤函数 时AM过椭圆的右焦点.其中所有的真命题是( )
时AM过椭圆的右焦点.其中所有的真命题是( )A.①③⑤
B.②③④
C.②③⑤
D.③④⑤
查看习题详情和答案>>
(2013•怀化二模)如图展示了一个由区间(0,k)(其中k为一正实数)到实数集R上的映射过程:区间(0,k)中的实数m对应线段AB上的点M,如图1;将线段AB围成一个离心率为
的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,

现给出下列5个命题①f(
)=6;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点(
,0)对称;⑤函数f(m)=3
时AM过椭圆的右焦点.其中所有的真命题是( )
| ||
| 2 |

现给出下列5个命题①f(
| k |
| 2 |
| k |
| 2 |
| 3 |
查看习题详情和答案>>