题目内容
下图展示了一个由区间 (其中
(其中 为一正实数)到实数集R上的映射过程:区间
为一正实数)到实数集R上的映射过程:区间 中的实数
中的实数 对应线段
对应线段 上的点
上的点 ,如图1;将线段
,如图1;将线段 围成一个离心率为
围成一个离心率为 的椭圆,使两端点
的椭圆,使两端点 、
、 恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在
恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在 轴上,已知此时点
轴上,已知此时点 的坐标为
的坐标为 ,如图3,在图形变化过程中,图1中线段
,如图3,在图形变化过程中,图1中线段 的长度对应于图3中的椭圆弧ADM的长度.图3中直线
的长度对应于图3中的椭圆弧ADM的长度.图3中直线 与直线
与直线 交于点
交于点 ,则与实数
,则与实数 对应的实数就是
对应的实数就是 ,记作
,记作 ,
,
现给出下列5个命题
① ; ②函数
; ②函数 是奇函数;③函数
是奇函数;③函数 在
在 上单调递增; ④.函数
上单调递增; ④.函数 的图象关于点
的图象关于点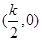 对称;⑤函数
对称;⑤函数 时AM过椭圆的右焦点.其中所有的真命题是: ( )
时AM过椭圆的右焦点.其中所有的真命题是: ( )
| A.①③⑤ | B.②③④ | C.②③⑤ | D.③④⑤ |
D
解析试题分析:本题可用排除法,由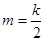 可知,点M位于线段AB的中点,则在图3中位于椭圆与y轴负半轴的交点,结合图像可知
可知,点M位于线段AB的中点,则在图3中位于椭圆与y轴负半轴的交点,结合图像可知 ,故①不对;由
,故①不对;由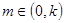 可知函数
可知函数 的定义域不关于原点对称,故函数
的定义域不关于原点对称,故函数 是非奇非偶函数,②不对; 在图3中点M在椭圆上逆时针移动时,点N在直线
是非奇非偶函数,②不对; 在图3中点M在椭圆上逆时针移动时,点N在直线 上自左向右移动
上自左向右移动 值增大,故知③正确;点N关于
值增大,故知③正确;点N关于 轴对称可知④正确;若
轴对称可知④正确;若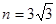 时,由点
时,由点 的坐标为
的坐标为 可得
可得 ,离心率为
,离心率为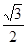 ,可知椭圆焦点坐标为
,可知椭圆焦点坐标为 ,
,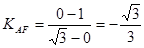 ,
,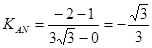 ,所以
,所以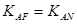 ,所以AM过椭圆的右焦点F,故⑤正确.
,所以AM过椭圆的右焦点F,故⑤正确.
考点:新定义的理解,奇偶函数的判别.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
函数 的零点所在的一个区间是 ( )
的零点所在的一个区间是 ( )
A. | B. | C. | D. |
函数 零点的个数是 ( )
零点的个数是 ( )
A. | B. | C. | D. |
定义在 上的奇函数
上的奇函数 ,满足
,满足 ,
, ,则函数
,则函数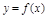 在区间
在区间 内零点个数的情况为( )
内零点个数的情况为( )
A. 个 个 | B. 个 个 | C. 个 个 | D.至少 个 个 |
偶函数 则关于
则关于 的方程
的方程 上解的个数是( )
上解的个数是( )
| A.l | B.2 | C.3 | D.4 |
函数 .满足
.满足 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
 ,若
,若 ,则称
,则称 为函数
为函数 ,则称
,则称 的“稳定点”恰是它的“不动点”,那么实数
的“稳定点”恰是它的“不动点”,那么实数 的取值范围是( )
的取值范围是( )



 在区间
在区间 上的简图是( )
上的简图是( )
 和
和 ,动点
,动点 在直线
在直线 上移动,椭圆
上移动,椭圆 以
以 为焦点且经过点
为焦点且经过点 ,记椭圆
,记椭圆 ,则函数
,则函数 的大致图像( )
的大致图像( )