摘要:15.如图所示边长是6的等边三角形纸片.撕成了不规则的甲.乙两部分.两张纸片间隔的水平距离是2.则中间留有空隙部分的面积是 .
网址:http://m.1010jiajiao.com/timu_id_767676[举报]
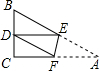 三角形纸片ABC,∠C=90°,AB=2BC=4.将纸片折叠使点A总是落在BC边上,记为点D,EF是折痕,如图所示.
三角形纸片ABC,∠C=90°,AB=2BC=4.将纸片折叠使点A总是落在BC边上,记为点D,EF是折痕,如图所示.(1)当△DEF是以∠EDF为顶角的等腰三角形时,四边形DFAE为哪种特殊的四边形?为什么?
(2)在(1)的条件下,求线段DF的长(结果用根号表示);
(3)在BC边上是否存在一点D,使以D,E,F为顶点的三角形和以D,E,B为顶点的三角形相似?若存在,求出相似比;若不存在,说明理由. 查看习题详情和答案>>
已知等边三角形纸片ABC的边长为8,D为AB边上的点,过点D作DG∥BC交AC于点G.DE⊥BC于点E,过点G作GF⊥BC于点F,把三角形纸片ABC分别沿DG,DE,GF按图1所示方式折叠,点A,B,C分别落在点A′,B′,C′处.若点A′,B′,C′在矩形DEFG内或其边上,且互不重合,此时我们称△A′B′C′(即图中阴影部分)为“重叠三角形”.
(1)若把三角形纸片ABC放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点A,B,C,D恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形A′B′C′的面积;
(2)实验探究:设AD的长为m,若重叠三角形A′B′C′存在.试用含m的代数式表示重叠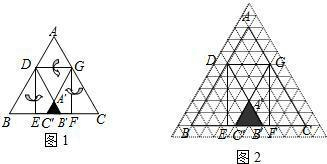 三角形A′B′C′的面积,并写出m的取值范围.(直接写出结果)
查看习题详情和答案>>
三角形A′B′C′的面积,并写出m的取值范围.(直接写出结果)
查看习题详情和答案>>
(1)若把三角形纸片ABC放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点A,B,C,D恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形A′B′C′的面积;
(2)实验探究:设AD的长为m,若重叠三角形A′B′C′存在.试用含m的代数式表示重叠
 三角形A′B′C′的面积,并写出m的取值范围.(直接写出结果)
查看习题详情和答案>>
三角形A′B′C′的面积,并写出m的取值范围.(直接写出结果)
查看习题详情和答案>>
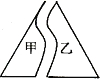 如图所示边长是6的等边三角形纸片,撕成了不规则的甲、乙两部分,两张纸片间隔的水平距离是2,则中间留有空隙部分的面积是
如图所示边长是6的等边三角形纸片,撕成了不规则的甲、乙两部分,两张纸片间隔的水平距离是2,则中间留有空隙部分的面积是 如图所示边长是6的等边三角形纸片,撕成了不规则的甲、乙两部分,两张纸片间隔的水平距离是2,则中间留有空隙部分的面积是________.
如图所示边长是6的等边三角形纸片,撕成了不规则的甲、乙两部分,两张纸片间隔的水平距离是2,则中间留有空隙部分的面积是________.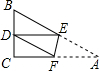 三角形纸片ABC,∠C=90°,AB=2BC=4.将纸片折叠使点A总是落在BC边上,记为点D,EF是折痕,如图所示.
三角形纸片ABC,∠C=90°,AB=2BC=4.将纸片折叠使点A总是落在BC边上,记为点D,EF是折痕,如图所示.