题目内容
 如图所示边长是6的等边三角形纸片,撕成了不规则的甲、乙两部分,两张纸片间隔的水平距离是2,则中间留有空隙部分的面积是________.
如图所示边长是6的等边三角形纸片,撕成了不规则的甲、乙两部分,两张纸片间隔的水平距离是2,则中间留有空隙部分的面积是________.
6
分析:首先根据题意画出撕开前的等边三角形的图形,求出面积,然后画出撕开后的图形,根据题意求出四边形EFBC的面积,最后撕开后四边形的面积减去等边三角形的面积,即得间隙部分的面积.
解答: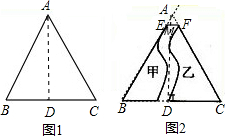 解:如图1,原等边三角形纸片为△A′B′C′,作A′D′⊥B′C′,
解:如图1,原等边三角形纸片为△A′B′C′,作A′D′⊥B′C′,
∵B′C′=6,∠B′=60°,
∴A′D′=3
∴S△A′B′C′=9 ,
,
撕开后的图形为图2,如图2,连接EF,延长BE,CF,设交于A点,作AD⊥BC于点D,
∵间隙为甲乙两部分平移分开后所产生的,
∴EF∥BC,
∴AD⊥EF,设垂足为M点,
∴∠AEF=∠AFE=60°,
∵EF=2,
∴BC=B′C′+2=6+2=8,AE=AF=2,
∵∠B=∠C=60°,
∴BA=AC=BC=8,
∴AN= ,AD=4
,AD=4 ,
,
∴S△ABC=16 ,S△AEF=
,S△AEF= ,
,
∴间隙部分的面积=S△ABC-S△AEF-S△A′B′C′=16 -9
-9 =6
=6 .
.
故答案为6 .
.
点评:本题主要考查等边三角形的性质,三角形的面积公式,关键在于根据图形正确的画出图形,作出相关三角形的高线,并求出相关三角形的面积.

分析:首先根据题意画出撕开前的等边三角形的图形,求出面积,然后画出撕开后的图形,根据题意求出四边形EFBC的面积,最后撕开后四边形的面积减去等边三角形的面积,即得间隙部分的面积.
解答:
 解:如图1,原等边三角形纸片为△A′B′C′,作A′D′⊥B′C′,
解:如图1,原等边三角形纸片为△A′B′C′,作A′D′⊥B′C′,∵B′C′=6,∠B′=60°,
∴A′D′=3

∴S△A′B′C′=9
 ,
,撕开后的图形为图2,如图2,连接EF,延长BE,CF,设交于A点,作AD⊥BC于点D,
∵间隙为甲乙两部分平移分开后所产生的,
∴EF∥BC,
∴AD⊥EF,设垂足为M点,
∴∠AEF=∠AFE=60°,
∵EF=2,
∴BC=B′C′+2=6+2=8,AE=AF=2,
∵∠B=∠C=60°,
∴BA=AC=BC=8,
∴AN=
 ,AD=4
,AD=4 ,
,∴S△ABC=16
 ,S△AEF=
,S△AEF= ,
,∴间隙部分的面积=S△ABC-S△AEF-S△A′B′C′=16
 -9
-9 =6
=6 .
.故答案为6
 .
.点评:本题主要考查等边三角形的性质,三角形的面积公式,关键在于根据图形正确的画出图形,作出相关三角形的高线,并求出相关三角形的面积.

练习册系列答案
相关题目
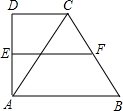 如图所示,直角梯形ABCD的一条对角线AC将梯形分成两个三角形,△ABC是边长为10的等边三角形,则梯形中位线EF=
如图所示,直角梯形ABCD的一条对角线AC将梯形分成两个三角形,△ABC是边长为10的等边三角形,则梯形中位线EF=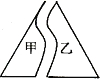 如图所示边长是6的等边三角形纸片,撕成了不规则的甲、乙两部分,两张纸片间隔的水平距离是2,则中间留有空隙部分的面积是
如图所示边长是6的等边三角形纸片,撕成了不规则的甲、乙两部分,两张纸片间隔的水平距离是2,则中间留有空隙部分的面积是 如图所示,△OAB是边长为
如图所示,△OAB是边长为 的位置时,请你在网格图中画出
的位置时,请你在网格图中画出
