摘要：A．点A B．点B C．点C D．点D
网址：http://m.1010jiajiao.com/timu_id_759825[举报]
如图，在平面直角坐标系中，矩形OABC的两边分别在x轴和y轴上，OA=10cm，OC=6cm．F是线段OA上的动点，从点O出发，以1cm/s的速度沿OA方向作匀速运动，点Q在线段AB上．已知A、Q两点间的距离是O、F两点间距离的a倍．若用（a，t）表示经过时间t（s）时，△OCF、△FAQ、△CBQ中有两个三角形全等．请写出（a，t）的所有可能情况 ．
查看习题详情和答案>>
查看习题详情和答案>>
如图，已知：△ABC中，
（1）只用直尺（没有刻度）和圆规求作一点P，使点P到三角形各边的距离都相等（要求保留作图痕迹，不必写出作法）．
（2）若△ABC中，AC=AB=4，∠CAB=120°，那么请计算以△ABC为轴截面的圆锥的侧面积（保留根号和π）．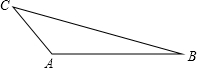
查看习题详情和答案>>
（1）只用直尺（没有刻度）和圆规求作一点P，使点P到三角形各边的距离都相等（要求保留作图痕迹，不必写出作法）．
（2）若△ABC中，AC=AB=4，∠CAB=120°，那么请计算以△ABC为轴截面的圆锥的侧面积（保留根号和π）．
查看习题详情和答案>>
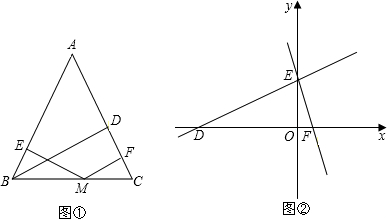
探索勾股定理时，我们发现“用不同的方式表示同一图形的面积”可以解决线段和（或差）的有关问题，这种方法称为面积法．请你运用面积法求解下列问题：在等腰三角形ABC中，AB=AC，BD为腰AC上的高．
（1）若BD=h，M是直线BC上的任意一点，M到AB、AC的距离分别为h1，h2．
A、若M在线段BC上，请你结合图形①证明：h1+h2=h；
B、当点M在BC的延长线上时，h1，h2，h之间的关系为 ．（请直接写出结论，不必证明）
（2）如图②，在平面直角坐标系中有两条直线l1：y=
x+6；l2：y=-3x+6．若l2上的一点M到l1的距离是3，请你利用以上结论求解点M的坐标．
查看习题详情和答案>>
（1）若BD=h，M是直线BC上的任意一点，M到AB、AC的距离分别为h1，h2．
A、若M在线段BC上，请你结合图形①证明：h1+h2=h；
B、当点M在BC的延长线上时，h1，h2，h之间的关系为
（2）如图②，在平面直角坐标系中有两条直线l1：y=
| 3 | 4 |
查看习题详情和答案>>
如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，点P是圆外一点，PA切⊙O于点A，且PA=PB．
已知抛物线y=-
（x+2）2+k与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，C点在y轴的正半轴上，线段OB、OC的长（OB＜OC）是方程x2-10x+16=0的两个根．
（1）求A、B、C三点的坐标；
（2）在平面直角坐标系内画出抛物线的大致图象并标明顶点坐标；
（3）连AC、BC，若点E是线段AB上的一个动点（与A、B不重合），过E作EF∥AC交BC于F，连CE，设AE=m，△CEF的面积为S，求S与m的函数关系式，并写出自变量m的取值范围；
（4）在（3）的基础上说明S是否存在最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由． 查看习题详情和答案>>
| 2 | 3 |
（1）求A、B、C三点的坐标；
（2）在平面直角坐标系内画出抛物线的大致图象并标明顶点坐标；
（3）连AC、BC，若点E是线段AB上的一个动点（与A、B不重合），过E作EF∥AC交BC于F，连CE，设AE=m，△CEF的面积为S，求S与m的函数关系式，并写出自变量m的取值范围；
（4）在（3）的基础上说明S是否存在最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由． 查看习题详情和答案>>