题目内容
探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的有关问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰三角形ABC中,AB=AC,BD为腰AC上的高.(1)若BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为h1,h2.
A、若M在线段BC上,请你结合图形①证明:h1+h2=h;
B、当点M在BC的延长线上时,h1,h2,h之间的关系为
(2)如图②,在平面直角坐标系中有两条直线l1:y=
| 3 | 4 |
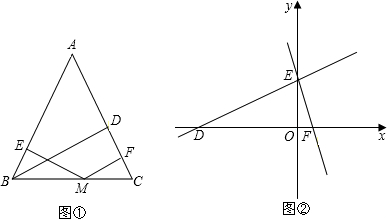
分析:(1)如图,连接AM,由于S△ABC=S△ABM+S△ACM,而EM⊥AB,MF⊥AC,BD⊥AC,因此得到
AC•h=
AB•h1+
AC•h2,而AB=AC,因此即可证明结论;
(2)由题意可知,DE=DF=10,所以△EDF是等腰三角形,
当点M在线段EF上时,依据(1)中结论,由h=EO=6可以得到M到DF(即x轴)的距离也为3,此时可求得M的坐标;
当点M在射线FE上时,依据(1)中结论,由h=EO=6可以得到M到DF(即x轴)的距离也为9,此时可求得M的坐标故点M的坐标为.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由题意可知,DE=DF=10,所以△EDF是等腰三角形,
当点M在线段EF上时,依据(1)中结论,由h=EO=6可以得到M到DF(即x轴)的距离也为3,此时可求得M的坐标;
当点M在射线FE上时,依据(1)中结论,由h=EO=6可以得到M到DF(即x轴)的距离也为9,此时可求得M的坐标故点M的坐标为.
解答: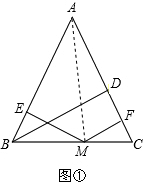 (1)证明:连接AM,
(1)证明:连接AM,
①∵S△ABC=S△ABM+S△ACM,EM⊥AB,MF⊥AC,BD⊥AC,
∴
AC•h=
AB•h1+
AC•h2,
又∵AB=AC,
∴h=h1+h2,(2分)
h1-h2=h;(3分)
故答案为:h1-h2=h.
(2)由题意可知,DE=DF=10,
∴△EDF是等腰三角形,(4分)
当点M在线段EF上时,依据(1)中结论,
∵h=EO=6,
∴M到DF(即x轴)的距离也为3,
∴点M的纵坐标为3,此时可求得M(1,3),(6分)
当点M在射线FE上时,依据(1)中结论,
∵h=EO=6,∴M到DF(即x轴)的距离也为9,
∴点M的纵坐标为9,此时可求得M(-1,9),(8分)
故点M的坐标为(1,3)或(-1,9).
 (1)证明:连接AM,
(1)证明:连接AM,①∵S△ABC=S△ABM+S△ACM,EM⊥AB,MF⊥AC,BD⊥AC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵AB=AC,
∴h=h1+h2,(2分)
h1-h2=h;(3分)
故答案为:h1-h2=h.
(2)由题意可知,DE=DF=10,

∴△EDF是等腰三角形,(4分)
当点M在线段EF上时,依据(1)中结论,
∵h=EO=6,
∴M到DF(即x轴)的距离也为3,
∴点M的纵坐标为3,此时可求得M(1,3),(6分)
当点M在射线FE上时,依据(1)中结论,
∵h=EO=6,∴M到DF(即x轴)的距离也为9,
∴点M的纵坐标为9,此时可求得M(-1,9),(8分)
故点M的坐标为(1,3)或(-1,9).
点评:此题分别考查了全等三角形的性质与判定、等腰三角形的性质、一次函数的性质等知识,题目要求学生有较高的综合解题能力,把几何图形的结论利用到函数图象中解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.
x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.
 x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.
x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.