题目内容
已知抛物线y=-| 2 | 3 |
(1)求A、B、C三点的坐标;
(2)在平面直角坐标系内画出抛物线的大致图象并标明顶点坐标;
(3)连AC、BC,若点E是线段AB上的一个动点(与A、B不重合),过E作EF∥AC交BC于F,连CE,设AE=m,△CEF的面积为S,求S与m的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上说明S是否存在最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
分析:(1)根据方程的两个根及函数的对称轴,易求A,B,C三点坐标;
(2)求出函数解析式,根据定点画出平滑的曲线;
(3)由勾股定理求出AC的长,由三角形内的平行关系,得到一个比例关系,从而求出EF,作辅助线把△CEF的面积用m表示出来,再求出其最值,并求出顶点坐标,也解决了第三问.
(2)求出函数解析式,根据定点画出平滑的曲线;
(3)由勾股定理求出AC的长,由三角形内的平行关系,得到一个比例关系,从而求出EF,作辅助线把△CEF的面积用m表示出来,再求出其最值,并求出顶点坐标,也解决了第三问.
解答:解:(1)方程x2-10x+16=0的两根为x1=8,x2=2,
∴OB=2,OC=8,
∴B(2,0)C(0,8)
∵函数y=-
(x+2)2+k的对称轴为x=-2,
∴A(-6,0),
即A(-6,0)B(2,0)C(0,8).(3分)
(2)B点在y=-
(x+2)2+k上,
∴0=-
(2+2)2+k,
∴k=
.(5分)
函数解析式为y=-
(x+2)2+
,
顶点坐标为-2,
),大致图象及顶点坐标如右.(7分)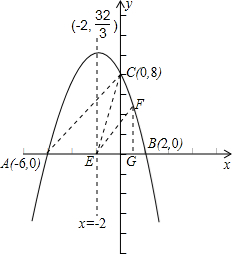
(3)∵AE=m,AB=8,
∴BE=8-m,
∵OC=8,OA=6,据勾股定理得AC=10,
∵AC∥EF,
∴
=
即
=
,EF=
,(10分)
过F作FG⊥AB于G,
∵sin∠CAB=sin∠FEB=
,
而sin∠FEB=
,
∴FG=8-m. 12分
∵S=S△CEB-S△FEB=
×BE×OC-
×BE×FG=-
m2+4m,
∴S与m的函数关系式为S=-
m2+4m,m的取值为0<m<8.
(4)∵S=-
m2+4m中-
<0,
∴S有最大值.
S=-
(m-4)2+8,当m=4时,S有最大值为8,
E点坐标为:E(-2,0),
∵B(2,0),E(-2-,0),
∴CE=CB
∴△BCE为等腰三角形.
∴OB=2,OC=8,
∴B(2,0)C(0,8)
∵函数y=-
| 2 |
| 3 |
∴A(-6,0),
即A(-6,0)B(2,0)C(0,8).(3分)
(2)B点在y=-
| 2 |
| 3 |
∴0=-
| 2 |
| 3 |
∴k=
| 23 |
| 3 |
函数解析式为y=-
| 2 |
| 3 |
| 23 |
| 3 |
顶点坐标为-2,
| 23 |
| 3 |
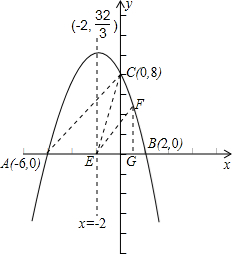
(3)∵AE=m,AB=8,
∴BE=8-m,
∵OC=8,OA=6,据勾股定理得AC=10,
∵AC∥EF,
∴
| AC |
| EF |
| AB |
| BE |
| 10 |
| EF |
| 8 |
| 8-m |
| 5(8-m) |
| 4 |
过F作FG⊥AB于G,
∵sin∠CAB=sin∠FEB=
| 4 |
| 5 |
而sin∠FEB=
| FG |
| EF |
∴FG=8-m. 12分
∵S=S△CEB-S△FEB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S与m的函数关系式为S=-
| 1 |
| 2 |
(4)∵S=-
| 1 |
| 2 |
| 1 |
| 2 |
∴S有最大值.
S=-
| 1 |
| 2 |
E点坐标为:E(-2,0),
∵B(2,0),E(-2-,0),
∴CE=CB
∴△BCE为等腰三角形.
点评:此题考查抛物线性质及对称轴,因图形很特殊,把具体问题转化到直角三角形中来解,注意直线平行的应用,最后把求面积最值转化到求函数最值问题,要学会这种做题思想.

练习册系列答案
相关题目
 (2011•金东区模拟)已知抛物线
(2011•金东区模拟)已知抛物线 B中点,点E是直线OC上的一个动点 (点E与点O不重合),点D在y轴上,且EO=ED.
B中点,点E是直线OC上的一个动点 (点E与点O不重合),点D在y轴上,且EO=ED.