摘要:(2)设AP=.(0<<2).△APF.△OEF的面积分别记为S1.S2,
网址:http://m.1010jiajiao.com/timu_id_744917[举报]
如图,在△ABC中,AB=BC=2,高BE=
,在BC边的延长线上取一点D,使CD=3.
(1)现有一动点P由A沿AB移动,设AP=t,S△PCD=S,求S与t之间的关系式及自变量t的取值范围.
(2)在(1)的条件下,当t=
时,过点C作CH⊥PD于H,设K=7CH:9PD.求证:关于x的二次函数y=-x2-(10k-
)x+2k的图象与x轴的两个交点关于原点对称.
(3)在(1)的条件下,是否存在正实数t,使PD边上的高CH=
CD?如果存在,请求出t的值;如果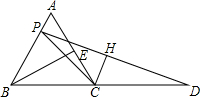 不存在,请说明理由.
查看习题详情和答案>>
不存在,请说明理由.
查看习题详情和答案>>
| 3 |
(1)现有一动点P由A沿AB移动,设AP=t,S△PCD=S,求S与t之间的关系式及自变量t的取值范围.
(2)在(1)的条件下,当t=
| 1 |
| 3 |
| 3 |
(3)在(1)的条件下,是否存在正实数t,使PD边上的高CH=
| 1 |
| 2 |
 不存在,请说明理由.
查看习题详情和答案>>
不存在,请说明理由.
查看习题详情和答案>>
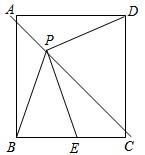 如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.设AP=x,△PBE的面积为y.则能够正确反映y与x之间的函数关系的图象是( )
如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.设AP=x,△PBE的面积为y.则能够正确反映y与x之间的函数关系的图象是( )A、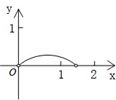 | B、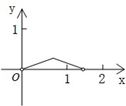 | C、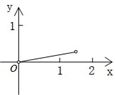 | D、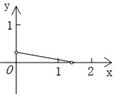 |
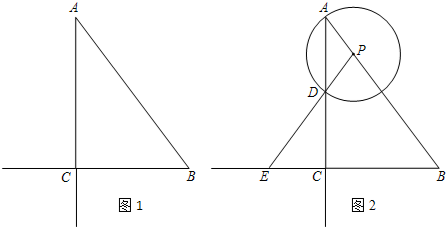
(2014•金山区一模)如图1,Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是斜边AB上的一个动点(点P与点A、B不重合),以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,射线PD交射线BC于点E.
(1)如图2,若点E在线段BC的延长线上,设AP=x,CE=y,
①求y关于x的函数关系式,并写出x的取值范围;
②当以BE为直径的圆和⊙P外切时,求AP的长;
(2)设线段BE的中点为Q,射线PQ与⊙P相交于点I,若CI=AP,求AP的长.
查看习题详情和答案>>
(1)如图2,若点E在线段BC的延长线上,设AP=x,CE=y,
①求y关于x的函数关系式,并写出x的取值范围;
②当以BE为直径的圆和⊙P外切时,求AP的长;
(2)设线段BE的中点为Q,射线PQ与⊙P相交于点I,若CI=AP,求AP的长.

 已知梯形ABCD中,AD∥BC,且AD<BC,AD=5,AB=DC=2.
已知梯形ABCD中,AD∥BC,且AD<BC,AD=5,AB=DC=2.