31．探究题——青夏教育精英家教网——

摘要：31．探究题

网址：http://m.1010jiajiao.com/timu_id_742926[举报]

探究题：
数学问题：各边长都是整数，最大边长为21的三角形有多少个？
为解决上面的数学问题，我们先研究下面的数学模型：
数学模型：在1～21这21个自然数中，每次取两个不同的数，使得所取的两个数之和大于21，有多少种不同取法？
为找到解决问题的方法，我们把上面数学模型简单化．
（1）在1～4这4个自然数中，每次取两个不同的数，使得所取的两个数之和大于4，有多少种取法？
根据题意，有下列取法：1+4，2+3，2+4，3+2，3+4，4+1，4+2，4+3，而1+4与4+1，2+3与3+2，…是同一种取法，所以上述每一种取法都重复过一次，因此共有

种不同的取法．
（2）在1～5这5个自然数中，每次取两个不同的数，使得所取的两个数之和大于5，有多少种取法？
根据题意，有下列取法：1+5，2+4，2+5，3+4，3+5，4+2，4+3，4+5，5+1，5+2，5+3，5+4，而1+5与5+1，2+4与4+2，…是同一种取法，所以上述每一种取法都重复过一次，因此共有

种不同的取法．
（3）在1～6这6个自然数中，每次取两个不同的数，使得所取的两个数之和大于6，有多少种不同的取法？
根据题意，有下列取法：1+6，2+5，2+6，3+4，3+5，3+6，4+3，4+5，4+6，5+2，5+3，5+4，5+6，6+1，6+2，6+3，6+4，6+5，而1+6与6+1，2+5与5+2，…是同一种取法，所以上述每一种取法都重复过一次，因此共有

种不同的取法．
（4）在1～7这7个自然数中，每次取两个不同的数，使得所取的两个数之和大于7，有多少种取法？
根据题意，有下列取法：1+7，2+6，2+7，3+5，3+6，3+7，4+5，4+6，4+7，5+3，5+4，5+6，5+7，6+2，6+3，6+4，6+5，6+7，7+1，7+2，7+3，7+4，7+5，7+6，而1+7与7+1，2+6与6+2，…是同一种取法，所以上述每一种取法都重复过一次，因此共有

种不同的取法…
问题解决
仿照上述研究问题的方法，解决上述数学模型和提出的问题
（1）在1～21这21个自然数中，每次取两个不同的数，使得所取的两个数之和大于21，共有

种不同取法；（只填结果）
（2）在1～n（n为偶数）这n个自然数中，每次取两个数，使得所取的两个数字之和大于n，共有

种不同取法；（只填最简算式）
（3）在1～n（n为奇数）这n个自然数中，每次取两个数，使得所取的两个数之和大于n，共有

种不同取法；（只填最简算式）
（4）各边长都是整数且不相等，最大边长为21的三角形有多少个？（写出最简算式和结果，不写分析过程）查看习题详情和答案>>

20、探究题：方格可以很方便的探究一些数学规律，现在请你用所给的方格解答下列问题．如图有一个△ABC．

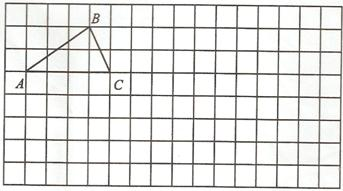
（1）请你在方格内画出满足条件A₁B₁=AB，B₁C₁=BC，C₁A₁=CA的△A₁B₁C₁；
（2）判断△A₁B₁C₁与△ABC是否一定全等？

查看习题详情和答案>>

28、探究题：
我们在前面学习过程中曾经接确过“弦图”，你能用四个全等的直角三角形画出弦图吗？相信你肯定会了；那么请你根据你掌握的知识解决下面的问题：
（1）试用边长分别为1cm和2cm的2个正方形剪拼成一个大的正方形，并画出示意图．
上面的问题你会了吧，那么你来试试解决下面的问题，相信自己肯定能行！
（2）下图是由5个相邻的正方形组成的一个长方形，试把它剪成一个正方形，画出示意图．

（3）请把一个宽为2，长为6.5的矩形纸片，剪拼成一个正方形，画出示意图．

（4）请把一个长为9，宽为4的矩形纸片，剪拼成一个正方形，画出示意图．

查看习题详情和答案>>

探究题：已知：1-

…
（1）观察上面式子的规律，请你猜测并写出第五项；
（2）上述的规律用一般的式子可以表示为：

（n为正整数）；试证明它的正确性；
（3）请直接用上述的结果计算

（x为正整数）的值．查看习题详情和答案>>

26、探究题．
如图，已知△ABC，∠BAC=90°，AB=AC，CD垂直于∠ABC角平分线BD于D，AC，BD交于E．AF为BC中线，交BE于G．
（1）求证：BE=2CD；
（2）CE和BG大小如何？不必证明．

查看习题详情和答案>>