题目内容
 26、探究题.
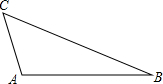
26、探究题.如图,已知△ABC,∠BAC=90°,AB=AC,CD垂直于∠ABC角平分线BD于D,AC,BD交于E.AF为BC中线,交BE于G.
(1)求证:BE=2CD;
(2)CE和BG大小如何?不必证明.
分析:(1)延长CE与BA延长线交于F.BD为角平分线:∠HBE=∠CBE∠BEH=∠BEC=90°(CE⊥BD).则CE=EF(这部分其实用BE是角平分线、高,同时也是中线来证明,即三线合一).CF=2CE∠BEH=90,∠AHC+∠ABD=∠ADB+∠ABD=90∠ADB=∠AHC,AB=AC.所以三角形ABD全等于ACF,则BD=CH、BD=2CE;
(2)根据图示直接回答.
(2)根据图示直接回答.
解答: 解:(1)证明:延长CD交BA延长线于H.
解:(1)证明:延长CD交BA延长线于H.
∵∠BAC=90°,CD⊥BD,
∴∠BAC=∠CDB=90°,又∠AEB=∠DEC,
∴△ABE∽△DCE,
∴∠ABD=∠ACD,
∵AB=AC,∠BAC=∠CAH=90°,
∴△ABE≌△ACH,
∴CH=BE;
∵BD平分∠ABC,
∴∠ABE=∠EBC,又∠BDH=∠BDC=90°,BD=BD,
∴△BHD≌△BDC,
∴CH=2CD,
∴BE=2CD;
(2)CE<BG.
 解:(1)证明:延长CD交BA延长线于H.
解:(1)证明:延长CD交BA延长线于H.∵∠BAC=90°,CD⊥BD,
∴∠BAC=∠CDB=90°,又∠AEB=∠DEC,
∴△ABE∽△DCE,
∴∠ABD=∠ACD,
∵AB=AC,∠BAC=∠CAH=90°,
∴△ABE≌△ACH,
∴CH=BE;
∵BD平分∠ABC,
∴∠ABE=∠EBC,又∠BDH=∠BDC=90°,BD=BD,
∴△BHD≌△BDC,
∴CH=2CD,
∴BE=2CD;
(2)CE<BG.
点评:本题考查了全等三角形的判定与性质、等腰直角三角形的性质、等腰三角形的判定与性质.本题通过作辅助线“延长CD交BA延长线于H”构建全等三角形来证明的.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 13、探究题:
13、探究题: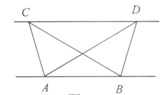
 的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.证明:MN∥EF.
的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.证明:MN∥EF.
 的图象上,且M(2,m),N是第三象限内反比例函数y=
的图象上,且M(2,m),N是第三象限内反比例函数y=
 中线,交BE于G.
中线,交BE于G.