摘要：20．本小题主要考查等差数列.等比数列的概念.等比数列的通项公式及前项和公式.考查运算能力和推理论证能力及分类讨论的思想方法．满分12分．(Ⅰ)证明:由题设.得.即．又..所以是首项为1.公比为的等比数列．...--．将以上各式相加.得．所以当时.上式对显然成立．.当时.显然不是与的等差中项.故．由可得.由得. ①整理得.解得或．于是．另一方面..．由①可得．所以对任意的.是与的等差中项．
网址：http://m.1010jiajiao.com/timu_id_73957[举报]
已知
是等差数列，其前n项和为
， 
是等比数列，且
（I）求数列与的通项公式；
（II）记
求证：
,
。
【考点定位】本小题主要考查等差数列与等比数列的概念、通项公式、前n项和公式、数列求和等基础知识.考查化归与转化的思想方法.考查运算能力、推理论证能力.
查看习题详情和答案>>
已知
是等差数列，其前n项和为
， 
是等比数列，且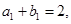
（I）求数列与的通项公式；
（II）记
求证：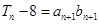
,
。
【考点定位】本小题主要考查等差数列与等比数列的概念、通项公式、前n项和公式、数列求和等基础知识.考查化归与转化的思想方法.考查运算能力、推理论证能力.
是等差数列，其前n项和为， 是等比数列，且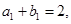 （I）求数列
与的通项公式；（II）记
求证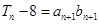：,。【考点定位】本小题主要考查等差数列与等比数列的概念、通项公式、前n项和公式、数列求和等基础知识.考查化归与转化的思想方法.考查运算能力、推理论证能力.
}的公差为d（d
0），等比数列{
}的公比为q（q>1）。设
=
+
…..+ 
,
=
=
= 1，d=2，q=3，求 
的值；
-（1+q）
=
，n
n
的两个不同的排列， 
， 
证明
。
}的公差为d（d
0），等比数列{
}的公比为q（q>1）。设
=
+
…..+ 
,
=
=
= 1，d=2，q=3，求 
的值；
-（1+q）
=
，n
n
的两个不同的排列， 
， 
证明
。