Question

（2009天津卷理）（本小题满分14分）

已知等差数列{}的公差为d（d0），等比数列{}的公比为q（q>1）。设=+…..+ ,=-+…..+(-1 ,n     

若== 1，d=2，q=3，求  的值；

若=1，证明（1-q）-（1+q）=，n；    

(Ⅲ)   若正数n满足2nq，设的两个不同的排列， ，   证明。

本小题主要考查等差数列的通项公式、等比数列的通项公式与前n项和公式等基础知识，考查运算能力，推理论证能力及综合分析和解决问题的能力的能力，满分14分。

Answer 1

（Ⅰ）解：由题设，可得

所以，     

（Ⅱ）证明：由题设可得则

                       ①

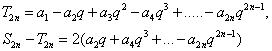                 ②

式减去②式，得    

     

式加上②式，得

                     ③

式两边同乘q，得

     

所以，

     

                               

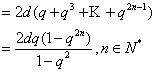
(Ⅲ)证明：   

                

因为所以

           

若，取i=n     

若，取i满足且

由（1）,(2)及题设知，且

    

当时，得

即，…，

又所以

     

因此

当同理可得，因此   

综上，