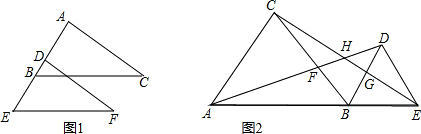
摘要:如下图.△ABC和△BDE是等边三角形.点A.B.D在一条直线上.并且AB=BD.由一个三角形变换到另一个三角形 A.仅能由平移得到 B.能由平移得到.也能由旋转得到 C.仅能由旋转得到 D.不能由平移得到.也不能由旋转得到
网址:http://m.1010jiajiao.com/timu_id_738085[举报]
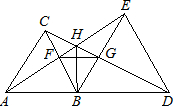 如图所示,已知△ABC和△BDE都是等边三角形,且A、B、D三点共线.下列结论:①AE=CD;②BF=BG;③HB平分∠AHD;④∠AHC=60°,⑤△BFG是等边三角形;⑥FG∥AD.其中正确的有
如图所示,已知△ABC和△BDE都是等边三角形,且A、B、D三点共线.下列结论:①AE=CD;②BF=BG;③HB平分∠AHD;④∠AHC=60°,⑤△BFG是等边三角形;⑥FG∥AD.其中正确的有
- A.3个
- B.4个
- C.5个
- D.6个
探究问题
(1)方法感悟:
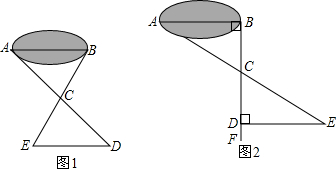
一班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
方案(Ⅰ)如图1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;感悟解题方法,并完成下列填空:
解:在如图所示的两个三角形△DEC和△ABC中:DC=AC,∠
(2)方法迁移:
方案(Ⅱ)如图2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.请你说明理由.
(3)问题拓展:
方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是
查看习题详情和答案>>
(1)方法感悟:
一班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
方案(Ⅰ)如图1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;感悟解题方法,并完成下列填空:
解:在如图所示的两个三角形△DEC和△ABC中:DC=AC,∠
ACB
ACB
=∠DCE
DCE
(对顶角相等),EC=BC,∴△DEC≌△ABC(SAS)
(SAS)
,∴DE=AB(全等三角形对应边相等),即DE的距离即为AB的长.(2)方法迁移:
方案(Ⅱ)如图2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.请你说明理由.
(3)问题拓展:
方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是
作∠ABC=∠EDC=90°
作∠ABC=∠EDC=90°
;若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ)是否成立?成立
成立
.
(1)填空:把下面的推理过程补充完整,并在括号内注明理由.
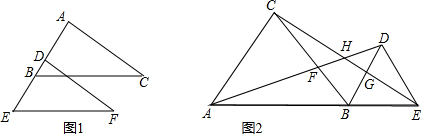
已知:如图1,BC∥EF,AB=DE,BC=EF,试说明∠C=∠F.
解:∵BC∥EF(已知)
∴∠ABC=
在△ABC与△DEF中

∴△ABC≌△DEF(
∴∠C=∠F(
(2)如图2,A、B、E三点在同一条直线上,△ABC和△BDE都是等边三角形,AD交BC于F,CE分别交BD、AD于G、H,请在图中找出三对全等三角形.
查看习题详情和答案>>

已知:如图1,BC∥EF,AB=DE,BC=EF,试说明∠C=∠F.
解:∵BC∥EF(已知)
∴∠ABC=
∠E
∠E
(两直线平行,同位角相等
两直线平行,同位角相等
)在△ABC与△DEF中

∴△ABC≌△DEF(
SAS
SAS
)∴∠C=∠F(
全等三角形的对应角相等
全等三角形的对应角相等
)(2)如图2,A、B、E三点在同一条直线上,△ABC和△BDE都是等边三角形,AD交BC于F,CE分别交BD、AD于G、H,请在图中找出三对全等三角形.