Question

（1）填空：把下面的推理过程补充完整，并在括号内注明理由．

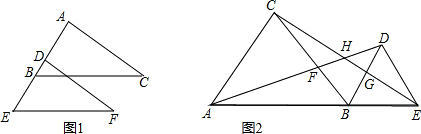
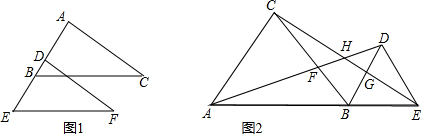
已知：如图1，BC∥EF，AB=DE，BC=EF，试说明∠C=∠F．
解：∵BC∥EF（已知）
∴∠ABC=________（________）
在△ABC与△DEF中

∴△ABC≌△DEF（________）
∴∠C=∠F（________）
（2）如图2，A、B、E三点在同一条直线上，△ABC和△BDE都是等边三角形，AD交BC于F，CE分别交BD、AD于G、H，请在图中找出三对全等三角形．

Answer 1

（1）证明：∵BC∥EF（已知），
∴∠ABC=∠E（两直线平行，同位角相等），
∵在△ABC和△DEF中
，
∴△ABC≌△DEF（SAS），
∴∠C=∠F（全等三角形的对应角相等），
故答案为：∠E，两直线平行，同位角相等，SAS，全等三角形的对应角相等．

（2）解：△ABD≌△CBE，△EBG≌△DBF，△ABF≌△CBG，
理由是：∵△ABC和△DBE都是等边三角形，
∴AB=BC，BD=BE，∠CBA=∠DBE，
∴∠CBA+∠CBD=∠DBE+∠CBD，
即∠ABD=∠CBE，
∵在△ABD和△CBE中
，
∴△ABD≌△CBE，
∴∠ADB=∠CEB，∠ECB=∠DAB，
∵∠CBA=∠DBE=60°，
∴∠CBD=180°-60°-60°=60°=∠DBE，
∵在△EBG和△DBF中
，
∴△EBG≌△DBF，
同理△ABF≌△CBG．
分析：（1）根据平行线的性质求出∠ABC=∠E，根据SAS求出△ABC≌△DEF，根据全等三角形的性质推出即可；
（2）根据等边三角形性质求出AB=BC，BD=BE，∠CBA=∠DBE，求出∠ABD=∠CBE，根据SAS证△ABD≌△CBE，推出∠ADB=∠CEB，∠ECB=∠DAB，根据ASA即可推出△EBG≌△DBF，△ABF≌△CBG．
点评：本题考查了等边三角形的性质，全等三角形的性质和判定，平行线的性质的应用，主要考查学生能否运用性质进行推理，题目比较典型，难度适中．