摘要：答案:四:1 (1)-3 (2) 2(1) (2) 3 (2)
网址：http://m.1010jiajiao.com/timu_id_72769[举报]
对于某些正整数n，存在A1，A2，…，An为集合{1，2，……，n}的n个不同子集，满足下列条件：对任意不大于n的正整数i，j，①
且每个Ai至少含有四个元素；②i∈Aj的充要条件是
(其中i≠j)．为了表示这些子集，作n行n列的数表，规定第i行第j列的数为
(1)求该数表中每列至多有多少个－1．
(2)用n表示该数表中1的个数，并证明n≥9
(3)请构造出集合{1，2，……，9}的9个不同子集A1，A2，…A9，使得A1，A2，…A9，满足题设(写出一种答案即可)．
定义{a，b，c}为函数y=ax2+bx+c的“特征数”．如：函数y=x2-2x+3的“特征数”是{1，-2，3}，函数y=2x+3的“特征数”是{0，2，3，}，函数y=-x的“特征数”是{0，-1，0}（1）将“特征数”是{0，
| ||
| 3 |
y=
x-1
| ||
| 3 |
y=
x-1
； （答案写在答卷上）
| ||
| 3 |
（2）在（1）中，平移前后的两个函数分别与y轴交于A、B两点，与直线x=
| 3 |
（3）若（2）中的四边形与“特征数”是{1，-2b，b2+
| 1 |
| 2 |
定义{a，b，c}为函数y=ax2+bx+c的“特征数”．如：函数y=x2-2x+3的“特征数”是{1，-2，3}，函数y=2x+3的“特征数”是{0，2，3，}，函数y=-x的“特征数”是{0，-1，0}
（1）将“特征数”是{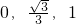
}的函数图象向下平移2个单位，得到的新函数的解析式是________； （答案写在答卷上）
（2）在（1）中，平移前后的两个函数分别与y轴交于A、B两点，与直线x=
分别交于D、C两点，在平面直角坐标系中画出图形，判断以点A、B、C、D为顶点的四边形形状，并说明理由；
（3）若（2）中的四边形与“特征数”是{
}的函数图象的有交点，求满足条件的实数b的取值范围．
查看习题详情和答案>>
请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效。
| |||
| |||
，
，
，
的标准差
为样本平均数
为底面面积，
为高
，
为球的半径第Ⅰ卷
一、选择题：本大题共12小题，每小题5分，满分60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知函数
的定义域为
，
的定义域为
，则
空集
2．已知复数
，则它的共轭复数等于
3．设变量
、
满足线性约束条件
，则目标函数
的最小值为
6 7 8 23
[选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．A．（选修4-1：几何证明选讲）
如图，圆O的直径AB=8，C为圆周上一点，BC=4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，求线段AE的长．
B．（选修4-2：矩阵与变换）
已知二阶矩阵A有特征值λ1=3及其对应的一个特征向量α1=
|
|
C．（选修4-4：坐标系与参数方程）
以平面直角坐标系的原点O为极点，x轴的正半轴为极轴，建立极坐标系（两种坐标系中取相同的单位长度），已知点A的直角坐标为（-2，6），点B的极坐标为(4，
| π |
| 2 |
| π |
| 4 |
D．（选修4-5：不等式选讲）
设a，b，c，d都是正数，且x=
| a2+b2 |
| c2+d2 |
| (ac+bd)(ad+bc) |