摘要：(2)设椭圆与轴正半轴.轴正半轴的交点分别为A.B.是否存在常数.使得向量与共线?如果存在.求的值,若不存在.请说明理由.
网址：http://m.1010jiajiao.com/timu_id_72603[举报]
一、选择题: B A B D A B D C B D Ｂ Ｃ
二、填空题： 13.
14．－８
15．1 16．①②
三、解答题：
18．解：依题意，第四项指标抽检合格的概率为 
其它三项指标抽检合格的概率均为
。
（1）若食品监管部门对其四项质量指标依次进行严格的检测，恰好在第三项指标检测结束时， 能确定该食品不能上市的概率等于第一、第二项指标中恰有一项不合格而且第三项指标不合格的概率．
(2)该品牌的食品能上市的概率等于四项指标都含格或第一、第二、第三项指标中仅有
一项不合格且第四项指标合格的概率．
故二面角
的大小为
解法二：如图，以
为原点，建立空间直角坐标系，使
轴，
、
分别在
轴、
轴上。
（1）由已知，
，
，
，
，
，
，
∴
， 
，
，
∵
， ∴
，
又
，∴
21.解：（1）设直线
的方程为
，联立，得
由△
得,
或
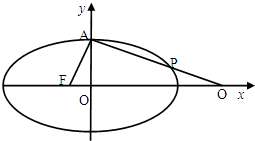设椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
| AP |
| 8 |
| 5 |
| PQ |
（1）求椭圆C的离心率；
（2）若过A、Q、F三点的圆恰好与直线l：x+
| 3 |
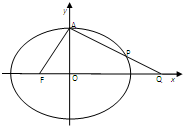设椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
| AP |
| 8 |
| 5 |
| PQ |
（1）求椭圆C的离心率；
（2）若过A、Q、F三点的圆恰好与直线l：x+
| 3 |
设椭圆C：
的左焦点为F，上顶点为A，过点A作垂直于AF的直线交椭圆C于另外一点P，交x轴正半轴于点Q， 且
（1）求椭圆C的离心率；
（2）若过A、Q、F三点的圆恰好与直线l： 
相切，求椭圆C的方程.
，其一个顶点的坐标是（1，0）．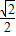
，其一个顶点的坐标是（1，0）．