网址:http://m.1010jiajiao.com/timu_id_72162[举报]
一、选择题(本大题共12小题,每小题5分,共60分)
BCDCA DCBBD BC
二、填空题(本大题共4小题,每小题4分,共16分)
13.24-----理科数学.files/image281.gif) 14.
14.-----理科数学.files/image283.gif) 15.5 16.4
15.5 16.4
三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17.解:(1)-----理科数学.files/image285.gif)
-----理科数学.files/image287.gif) =0
=0
-----理科数学.files/image289.gif)
由正弦定理得:-----理科数学.files/image291.gif) ,
,
-----理科数学.files/image293.gif)
若-----理科数学.files/image295.gif) 因为
因为-----理科数学.files/image297.gif) 所以
所以-----理科数学.files/image299.gif) ,故
,故-----理科数学.files/image301.gif)
若-----理科数学.files/image303.gif) ,因为
,因为-----理科数学.files/image305.gif) ,所以
,所以-----理科数学.files/image307.gif) ,故
,故-----理科数学.files/image309.gif)
综上-----理科数学.files/image301.gif) 或
或-----理科数学.files/image312.gif)
18.解:(1)-----理科数学.files/image314.gif)
-----理科数学.files/image316.gif) 当
当-----理科数学.files/image318.gif) 时,
时,-----理科数学.files/image320.gif)
两式相减得-----理科数学.files/image322.gif)
即-----理科数学.files/image324.gif)
-----理科数学.files/image316.gif) 当
当-----理科数学.files/image318.gif) 时,数列
时,数列-----理科数学.files/image030.gif) 是等比数列
是等比数列
要使数列-----理科数学.files/image030.gif) 是等比数列,
是等比数列,
当且仅当-----理科数学.files/image330.gif) ,即
,即-----理科数学.files/image332.gif)
从而-----理科数学.files/image334.gif)
(2)设数列-----理科数学.files/image194.gif) 的公差为
的公差为-----理科数学.files/image337.gif)
由-----理科数学.files/image199.gif) 得
得-----理科数学.files/image340.gif)
故可设-----理科数学.files/image342.gif)
又-----理科数学.files/image344.gif)
右题意知-----理科数学.files/image346.gif)
解得-----理科数学.files/image348.gif)
又等差数列-----理科数学.files/image194.gif) 的前
的前-----理科数学.files/image032.gif) 项和
项和-----理科数学.files/image197.gif) 有最大值,
有最大值,
-----理科数学.files/image353.gif)
从而-----理科数学.files/image355.gif)
19.解:(1)-----理科数学.files/image357.gif) 平面
平面-----理科数学.files/image223.gif)
证明:因为-----理科数学.files/image360.gif) 平面
平面-----理科数学.files/image362.gif) ,所以
,所以-----理科数学.files/image364.gif) ,
,
又在-----理科数学.files/image204.gif) 中,
中,-----理科数学.files/image367.gif) ,所以,
,所以,-----理科数学.files/image369.gif) 又
又-----理科数学.files/image371.gif)
所以,-----理科数学.files/image373.gif) 平面
平面-----理科数学.files/image223.gif) ,
,
又在-----理科数学.files/image376.gif) 中,
中,-----理科数学.files/image210.gif) 、
、-----理科数学.files/image212.gif) 分别是
分别是-----理科数学.files/image214.gif) 、
、-----理科数学.files/image216.gif) 上的动点,且
上的动点,且-----理科数学.files/image218.gif)
-----理科数学.files/image383.gif)
-----理科数学.files/image385.gif) 平面
平面-----理科数学.files/image387.gif) 平面
平面-----理科数学.files/image223.gif) ,
,
所以,不论-----理科数学.files/image390.gif) 为何值,总有
为何值,总有-----理科数学.files/image357.gif) 平面
平面-----理科数学.files/image223.gif) ;
;
(2)解:在-----理科数学.files/image204.gif) 中,
中,-----理科数学.files/image367.gif) ,
,-----理科数学.files/image396.gif) ,所以,
,所以,-----理科数学.files/image398.gif)
又-----理科数学.files/image360.gif) 平面
平面-----理科数学.files/image362.gif) ,所以
,所以-----理科数学.files/image402.gif) ,
,
又在-----理科数学.files/image404.gif) 中,
中,-----理科数学.files/image406.gif) ,
,-----理科数学.files/image408.gif)
由(1)知-----理科数学.files/image357.gif) 平面
平面-----理科数学.files/image411.gif) ,
,-----理科数学.files/image413.gif)
-----理科数学.files/image415.gif)
所以,三棱锥-----理科数学.files/image227.gif) 的体积是
的体积是-----理科数学.files/image418.gif)
20.解:(1)-----理科数学.files/image229.gif) 的所有可能取值为0,1,2,依题意得:
的所有可能取值为0,1,2,依题意得:
-----理科数学.files/image421.gif)
-----理科数学.files/image423.gif) 的分布列为
的分布列为
-----理科数学.files/image229.gif)
0
1
2
P
-----理科数学.files/image087.gif)
-----理科数学.files/image091.gif)
-----理科数学.files/image087.gif)
-----理科数学.files/image429.gif)
(2)设“甲、乙都不被选中”的事件为-----理科数学.files/image247.gif) ,则
,则-----理科数学.files/image432.gif)
-----理科数学.files/image316.gif) 所求概率为
所求概率为-----理科数学.files/image435.gif)
(3)记“男生甲被选中”为事件-----理科数学.files/image012.gif) ,“女生乙被选中”为事件
,“女生乙被选中”为事件-----理科数学.files/image014.gif) ,
,
-----理科数学.files/image439.gif)
-----理科数学.files/image441.gif) (或直接得
(或直接得-----理科数学.files/image443.gif) )
)
21.解:(1)甲-----理科数学.files/image445.gif) 得
得-----理科数学.files/image242.gif) 是
是-----理科数学.files/image448.gif) 的中点
的中点
设-----理科数学.files/image450.gif) 依题意得:
依题意得:
-----理科数学.files/image452.gif)
消去-----理科数学.files/image454.gif) ,整理得
,整理得-----理科数学.files/image456.gif)
当-----理科数学.files/image255.gif) 时,方程表示焦点在
时,方程表示焦点在-----理科数学.files/image159.gif) 轴上的椭圆;
轴上的椭圆;
当-----理科数学.files/image460.gif) 时,方程表示焦点在
时,方程表示焦点在-----理科数学.files/image155.gif) 轴上的椭圆;
轴上的椭圆;
当-----理科数学.files/image463.gif) 时,方程表示圆。
时,方程表示圆。
(Ⅱ)由-----理科数学.files/image255.gif) ,焦点在
,焦点在-----理科数学.files/image159.gif) 轴上的椭圆,直线
轴上的椭圆,直线-----理科数学.files/image251.gif) 与曲线
与曲线-----理科数学.files/image247.gif) 恒有两交点,
恒有两交点,
因为直线斜率不存在时不符合题意,
可设直线-----理科数学.files/image251.gif) 的方程为
的方程为 -----理科数学.files/image470.gif) ,直线与椭圆的交点为
,直线与椭圆的交点为-----理科数学.files/image472.gif)
-----理科数学.files/image474.gif)
-----理科数学.files/image476.gif)
-----理科数学.files/image478.gif)
要使-----理科数学.files/image257.gif) 为锐角,则有
为锐角,则有-----理科数学.files/image481.gif)
-----理科数学.files/image483.gif)
即-----理科数学.files/image485.gif)
可得-----理科数学.files/image487.gif) ,对于任意
,对于任意-----理科数学.files/image255.gif) 恒成立
恒成立
而-----理科数学.files/image490.gif) 。
。
所以满足条件的-----理科数学.files/image169.gif) 的取值范围是
的取值范围是-----理科数学.files/image493.gif)
22.解:(1)当-----理科数学.files/image495.gif) 时,
时,-----理科数学.files/image497.gif)
所以,-----理科数学.files/image265.gif) 在
在-----理科数学.files/image267.gif) 上是单调递增,
上是单调递增,-----理科数学.files/image501.gif)
(2)-----理科数学.files/image271.gif) 的定义域是
的定义域是-----理科数学.files/image267.gif)
-----理科数学.files/image505.gif)
当-----理科数学.files/image507.gif) 时,
时,-----理科数学.files/image509.gif) ,所以,
,所以,-----理科数学.files/image511.gif)
当-----理科数学.files/image513.gif) 时,
时,-----理科数学.files/image515.gif) ,所以,
,所以,-----理科数学.files/image517.gif) ,
,
所以,在-----理科数学.files/image519.gif) 上
上-----理科数学.files/image271.gif) 单调递减,在
单调递减,在-----理科数学.files/image522.gif) 上,
上,-----理科数学.files/image271.gif) 单调递增,
单调递增,
所以,-----理科数学.files/image525.gif)
(3)由(2)知-----理科数学.files/image271.gif) 在
在-----理科数学.files/image528.gif) 上是单调递增函数,
上是单调递增函数,
若存在-----理科数学.files/image273.gif) 满足条件,则必有
满足条件,则必有-----理科数学.files/image531.gif) ,
,
也即方程-----理科数学.files/image533.gif) 在
在-----理科数学.files/image528.gif) 上有两个不等的实根
上有两个不等的实根-----理科数学.files/image273.gif)
但方程-----理科数学.files/image537.gif) 即
即-----理科数学.files/image539.gif) 只有一个实根
只有一个实根-----理科数学.files/image541.gif)
所以,不存在满足条件的实数-----理科数学.files/image273.gif)
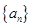 的前
的前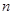 项和记为
项和记为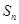 ,
, ,
,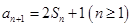 .
.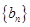 的前
的前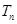 有最大值,且
有最大值,且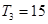 ,又
,又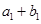 、
、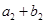 、
、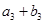 成等比数列,求
成等比数列,求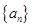 的前
的前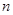 项和记为
项和记为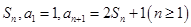
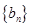 的各项为正,其前
的各项为正,其前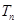 ,且
,且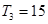 ,又
,又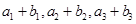 成等比数列,求
成等比数列,求 的前
的前 项和记为
项和记为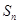 ,
, ,
, .
. 为何值时,数列
为何值时,数列 的前
的前 有最大值,且
有最大值,且 ,又
,又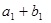 ,
, ,
, 成等比数列,求
成等比数列,求 .
.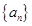 的前
的前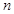 项和记为
项和记为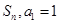 ,
,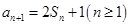
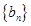 的各项为正,其前
的各项为正,其前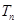 ,且
,且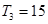 ,又
,又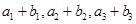 成等比数列,求
成等比数列,求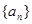 的前
的前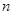 项和记为
项和记为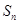 ,
,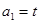 ,点
,点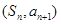 在直线
在直线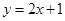 上,
上,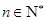 .
.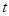 为何值时,数列
为何值时,数列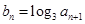 ,
,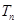 是数列
是数列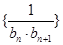 的前
的前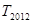 的值.
的值.