题目内容
数列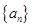 的前
的前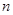 项和记为
项和记为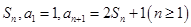
(Ⅰ)求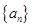 的通项公式;
的通项公式;
(Ⅱ)等差数列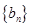 的各项为正,其前
的各项为正,其前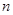 项和为
项和为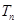 ,且
,且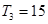 ,又
,又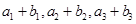 成等比数列,求
成等比数列,求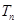
【答案】
(Ⅰ) (Ⅱ)
(Ⅱ)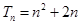
【解析】
试题分析:(Ⅰ)由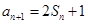 可得
可得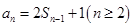 ,两式相减得
,两式相减得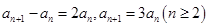 3分
3分
又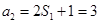 ∴
∴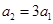
故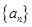 是首项为
是首项为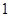 ,公比为
,公比为 得等比数列
得等比数列
∴ 6分
6分
(Ⅱ)设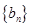 的公差为
的公差为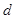
由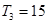 得,可得
得,可得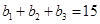 ,可得
,可得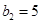
故可设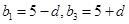
又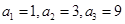
由题意可得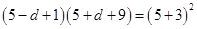
解得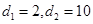
∵等差数列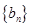 的各项为正,∴
的各项为正,∴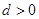
∴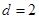 10分
10分
∴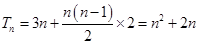 12分
12分
考点:等差数列等比数列性质及由数列前n项和求通项
点评:由前n项和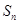 求通项
求通项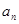 时需分情况讨论:
时需分情况讨论: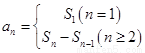 ,最终看其结果能否合并为一个关系式
,最终看其结果能否合并为一个关系式

练习册系列答案
相关题目
 的前
的前 项和记为
项和记为 ,
, ,点
,点 在直线
在直线 上,
上, .
. 为何值时,数列
为何值时,数列 ,
,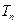 是数列
是数列 的前
的前 的值.
的值. 的前
的前 项和记为
项和记为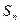 ,
,
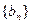 的各项为正,其前
的各项为正,其前 ,且
,且 ,
, 的前
的前 项和记为
项和记为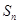 ,
, ,
, .
. 为何值时,数列
为何值时,数列 的前
的前 有最大值,且
有最大值,且 ,又
,又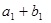 ,
, ,
, 成等比数列,求
成等比数列,求 .
.