题目内容
数列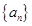 的前
的前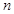 项和记为
项和记为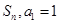 ,
,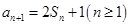
(Ⅰ)求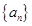 的通项公式;
的通项公式;
(Ⅱ)等差数列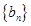 的各项为正,其前
的各项为正,其前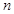 项和为
项和为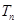 ,且
,且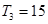 ,又
,又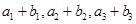 成等比数列,求
成等比数列,求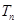 .
.
【答案】
(1) ;(2)
;(2)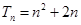 .
.
【解析】本试题主要考查了舒蕾的通项公式和求和的运用。第一问中利用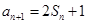 ,得到
,得到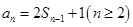 ,两式相减得
,两式相减得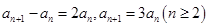 ,故可知故
,故可知故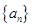 是首项为
是首项为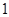 、公比为
、公比为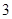 的等比数列, ∴
的等比数列, ∴
(2)中利用由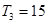 得,可得
得,可得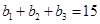 ,可得
,可得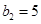 故可设
故可设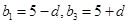 ,解得
,解得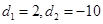 ,利用等差数列的前n项和公式可知∵等差数列
,利用等差数列的前n项和公式可知∵等差数列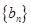 的各项为正,∴
的各项为正,∴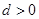 , ∴
, ∴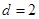
∴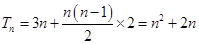
解:(Ⅰ)由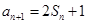 可得
可得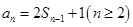 ,
,
两式相减得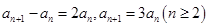
又 , ∴
, ∴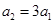
故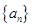 是首项为
是首项为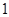 、公比为
、公比为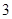 的等比数列, ∴
的等比数列, ∴
(Ⅱ)设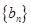 的公比为
的公比为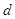 ,由
,由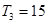 得,可得
得,可得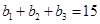 ,可得
,可得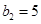
故可设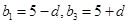 , 又
, 又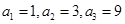
由题意可得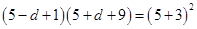 ,解得
,解得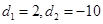
∵等差数列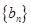 的各项为正,∴
的各项为正,∴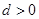 , ∴
, ∴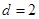
∴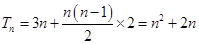

练习册系列答案
相关题目
 的前
的前 项和记为
项和记为 ,
, ,点
,点 在直线
在直线 上,
上, .
. 为何值时,数列
为何值时,数列 ,
,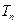 是数列
是数列 的前
的前 的值.
的值. 的前
的前 项和记为
项和记为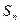 ,
,
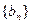 的各项为正,其前
的各项为正,其前 ,且
,且 ,
, 的前
的前 项和记为
项和记为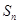 ,
, ,
, .
. 为何值时,数列
为何值时,数列 的前
的前 有最大值,且
有最大值,且 ,又
,又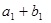 ,
, ,
, 成等比数列,求
成等比数列,求 .
.