摘要：4．若点P(x.y)在第四象限.且=3.,=5.则点P的坐标为 A． B． C． D．(3.5)
网址：http://m.1010jiajiao.com/timu_id_692635[举报]
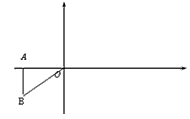
如图， 
中，O是坐标原点，A
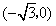，B
，
（1）以原点O为位似中心，将
放大，使变换后得到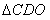
的与
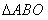的位似比为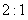
， 且D在第一象限内，则C点坐标为（ ____，____）； D点坐标为（____，____）；
（2）将（1）中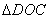
沿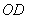
折叠，点C落在第一象限的E处，画出图形，并求出点E的坐标；
（3）若抛物线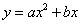
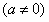过（2）中的E、C两点，求抛物线的解析式；
（4）在（3）中的抛物线EC段（不包括C、E点）上是否存在一点M，使得四边形MEOC面积最大？若存在，求出这个最大值，并求出此时M点的坐标；若不存在，请说明理由。
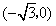中，O是坐标原点，A，B，（1）以原点O为位似中心，将
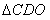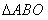放大，使变换后得到的与的位似比为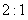， 且D在第一象限内，则C点坐标为（ ____，____）； D点坐标为（____，____）；（2）将（1）中
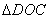沿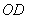折叠，点C落在第一象限的E处，画出图形，并求出点E的坐标；（3）若抛物线
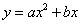
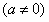过（2）中的E、C两点，求抛物线的解析式；（4）在（3）中的抛物线EC段（不包括C、E点）上是否存在一点M，使得四边形MEOC面积最大？若存在，求出这个最大值，并求出此时M点的坐标；若不存在，请说明理由。
已知直线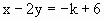
和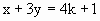
，若它们的交点在第四象限内．
(1)则k的取值范围是____<K<______；
(2)若k为非负整数，点A的坐标为(2，0)，点P在直线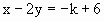
上，且
为等腰三角形，OA为底．则点P的坐标是（____,____)
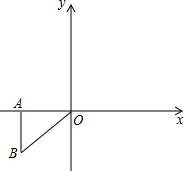如图，△ABO中，O是坐标原点，A(-| 3 |
| 3 |
（1）①以原点O为位似中心，将△ABO放大，使变换后得到的△CDO与△ABO的位似比为2：1，且D在第一象限内，则C点坐标为（
②将△DOC沿OD折叠，点C落在第一象限的E处，画出图形，并求出点E的坐标；
（2）若抛物线y=ax2+bx（a≠0）过（1）中的E、C两点，求抛物线的解析式；
（3）在（2）中的抛物线EC段（不包括C、E点）上是否存在一点M，使得四边形MEOC面积最大？若存在，求出这个最大值，并求出此时M点的坐标；若不存在，请说明理由． 查看习题详情和答案>>
(1)若函数：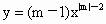
是反比例函数，则m的值为_________．
(2)反比例函数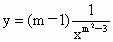
的图象在二、四象限，则m=___________．
(3)如果点(a，－2a)在函数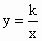
的图象上，那么k________0(填“＞”或“＜”)．
(4)函数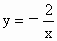
的图象在第_________象限，在每一象限内，y随x的增大而_________．
(5)已知y与x成反比例，并且x=2时，y=1；则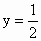
时，x=_______．
已知点P的坐标为（m，0），在x轴上存在点Q（不与P点重合），以PQ为边作正方形PQMN，使点M落在反比例函数y=-
的图象上。小明对上述问题进行了探究，发现不论m取何值，符合上述条件的正方形只有两个，且一个正方形的顶点M在第四象限，另一个正方形的顶点M1在第二象限。
的图象上。小明对上述问题进行了探究，发现不论m取何值，符合上述条件的正方形只有两个，且一个正方形的顶点M在第四象限，另一个正方形的顶点M1在第二象限。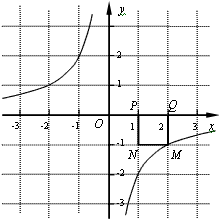
（1）如图所示，若反比例函数解析式为y=-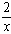
，P点坐标为（1，0），图中已画出一符合条件的一个正方形PQMN，请你在图中画出符合条件的另一个正方形PQ1M1N1，并写出点M1的坐标；M1的坐标是____。
（2）请你通过改变P点坐标，对直线M1M的解析式y=kx+b进行探究可得k=______，若点P的坐标为（m，0）时，则b=______；
（3）依据（2）的规律，如果点P的坐标为（6，0），请你求出点M1和点M的坐标。
查看习题详情和答案>>
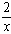，P点坐标为（1，0），图中已画出一符合条件的一个正方形PQMN，请你在图中画出符合条件的另一个正方形PQ1M1N1，并写出点M1的坐标；M1的坐标是____。（2）请你通过改变P点坐标，对直线M1M的解析式y=kx+b进行探究可得k=______，若点P的坐标为（m，0）时，则b=______；
（3）依据（2）的规律，如果点P的坐标为（6，0），请你求出点M1和点M的坐标。